Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
b: Xét ΔOAD vuông tại A và ΔOBC vuông tại B có
OA=OB
\(\widehat{BOC}\) chung
Do đó: ΔOAD=ΔOBC
Suy ra: OD=OC
Xét ΔOIC và ΔOID có
OC=OD
\(\widehat{COI}=\widehat{DOI}\)
OI chung
Do đó: ΔOIC=ΔOID
c: Ta có: ΔOCD cân tại O
mà OI là đường phân giác
nên OI là đường cao
a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
b: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB vuông góc Oy
c: OA=OB
CA=CB
=>OC là trung trực của AB
a: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
b: Xét ΔOBC vuông tại B và ΔOAD vuông tại A có
OB=OA
\(\widehat{BOC}\) chung
Do đó: ΔOBC=ΔOAD
Suy ra: OC=OD
Xét ΔOIC và ΔOID có
OI chung
\(\widehat{COI}=\widehat{DOI}\)
OC=OD
Do đó: ΔOIC=ΔOID
c: Ta có: ΔOCD cân tại O
mà OI là đường phân giác
nên OI là đường cao
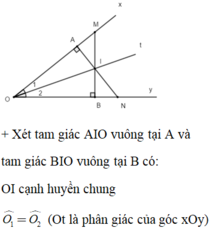
Do đó: Δ A I O = Δ B I O (cạnh huyền – góc nhọn)
Suy ra OA = OB ; IA = IB (hai cạnh tương ứng)
+ Xét tam giác IAM vuông tại A và tam giác IBN vuông tại B có:
IA = IB (cmt)
Bài 2:
a) Xét ΔABI vuông tại A và ΔEBI vuông tại E có
BI chung
\(\widehat{ABI}=\widehat{EBI}\)(BI là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABI=ΔEBI(cạnh huyền-góc nhọn)
Suy ra: BA=BE(hai cạnh tương ứng)
Xét ΔBAE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Xét ΔBAE cân tại B có \(\widehat{ABE}=60^0\)(gt)
nên ΔBAE đều(Dấu hiệu nhận biết tam giác đều)
b) Ta có: ΔABI=ΔEBI(cmt)
nên IA=IE(hai cạnh tương ứng)
Xét ΔIAE có IA=IE(cmt)
nên ΔIAE cân tại I(Định nghĩa tam giác cân)
c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Vậy: AC=4cm
Bài 5:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE
Ox (A
Ox)