Cho tam giác ABC vuông tại A. Gọi N là trung điểm của BC, D là trung điểm của AC. Lấy M là điểm đối xứng với N qua D.
Tứ giác ANCM là hình gì? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2021
a: Xét ΔABC có
N là trung điểm của BC
D là trung điểm của AC
Do đó: ND là đường trung bình của ΔABC
Suy ra: ND//AB
hay ND⊥AC
13 tháng 1 2022
a: Xét tứ giác AIME có
\(\widehat{AIM}=\widehat{AEM}=\widehat{EAI}=90^0\)
Do đó: AIME là hình chữ nhật
b: Xét tứ giác ANCM có
I là trung điểm của AC
I là trung điểm của NM
Do đó: ANCM là hình bình hành
mà MA=MC
nên ANCM là hình thoi
c: Để AIME là hình vuông thì AI=AE
hay AB=AC
CH
Cô Hoàng Huyền
Admin
VIP
26 tháng 2 2018
Em tham khảo tại đây nhé.
Câu hỏi của nguuen thi minh tam - Toán lớp 8 - Học toán với OnlineMath
CM
27 tháng 8 2018
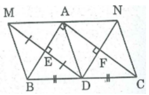
Điểm M và điểm D đối xứng qua trục AB
Suy ra AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM ⇒ ∠ (AED) = 90 0
Điểm D và điểm N đối xứng qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN ⇒ AC ⊥ DN ⇒ ∠ (AFD) = 90 0
Mà ∠ (EAF) = 90 0 (gt). Vậy tứ giác AEDF là hình chữ nhật (vì có 3 góc vuông).
1 tháng 1 2022
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
Xét tứ giác ANCM có
D là trung điểm của AC
D là trung điểm của NM
Do đó: ANCM là hình bình hành
mà AN=CN
nên ANCM là hình thoi