Cho tam giác ABC có góc A bằng 90 độ. Vẽ đường thẳng AH vuông góc với BC (H thuộc BC). Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD
a. Chứng minh tam giác AHB = tam giác DBH
b. Hai đường thẳng AB và DH có song song không? Vì sao?
c. Tính góc ACB biết góc BAH = 35 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác AHB và tam giác DBH có:
AH=BD (giả thiết)
Góc AHB=góc DBH (=90o)
BH là cạnh chung
=> Tam giác AHB = tam giác DBH (c.g.c)
b) Theo chứng minh phần a: Tam giác AHB = tam giác DBH => Góc ABH = góc BHD (2 góc tương ứng)
Mà góc ABH và góc BHD là 2 góc so le trong => AB//DH
c) Tam giác ABH có: \(\widehat{BAH}+\widehat{AHB}+\widehat{ABH}=180^o\) (tổng 3 góc trong tam giác)
=>\(35^o+90^o+\widehat{ABH}=180^o\Rightarrow\widehat{ABH}=180^o-35^o-90^o=55^o\)
Tam giác ABC có: \(\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^o\)(tổng 3 góc trong tam giác)
=>\(90^o+\widehat{ACB}+55^o=180^o\Rightarrow\widehat{ACB}=180^o-90^o-55^o=35^o\)

Gợi ý:
a) Tam giác AHB= Tam giác DBH (c-g-c) vì có góc H=góc B, BH là cạnh chung, AH=BD.
b) Tam giác AHB= Tam giác DBH => góc DHB=ABH mà 2 góc nằm so le trong nên AB//HD.
c) Tam giác BCD= Tam giác HCA (g-c-g) vì có góc BDC=góc HAC (AB//HD), góc B= góc H, BD=AH. => O t/đ BH.
d) góc BDH=750=> góc BHD=150=>góc ABC=150=>góc ACB là góc vuông.

Câu hỏi của Lê Thu Phương Anh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
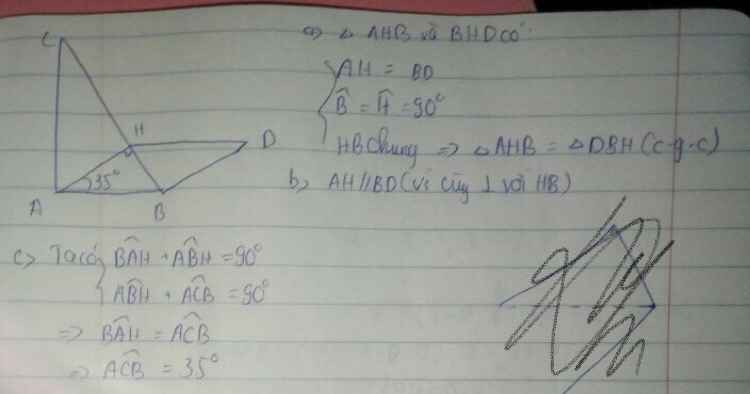
chào cậu
45 nhé mk tính đó chắc cũng sai đó nhưng mk tính mãi rùi