rút gọn biểu thức sau : A = 1+1/22+1/23+...+1/22015
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
31 tháng 12 2023
1/
Tổng A là tổng các số hạng cách đều nhau 4 đơn vị.
Số số hạng: $(101-1):4+1=26$
$A=(101+1)\times 26:2=1326$
AH
Akai Haruma
Giáo viên
31 tháng 12 2023
2/
$B=(1+2+2^2)+(2^3+2^4+2^5)+(2^6+2^7+2^8)+(2^9+2^{10}+2^{11})$
$=(1+2+2^2)+2^3(1+2+2^2)+2^6(1+2+2^2)+2^9(1+2+2^2)$
$=(1+2+2^2)(1+2^3+2^6+2^9)$
$=7(1+2^3+2^6+2^9)\vdots 7$
28 tháng 9 2023
`#3107`
\(A=1+2^1+2^2+2^3+...+2^{2015}\)
\(2A=2+2^2+2^3+2^4+...+2^{2016}\)
\(2A-A=\left(2+2^2+2^3+2^4+...+2^{2016}\right)-\left(1+2+2^2+2^3+...+2^{2015}\right)\)
\(A=2+2^2+2^3+2^4+...+2^{2016}-1-2-2^2-2^3-...-2^{2015}\)
\(A=2^{2016}-1\)
Vậy, \(A=2^{2016}-1.\)
28 tháng 9 2023
\(A=2^0+2^1+2^2+...+2^{2015}\)
\(2\cdot A=2^1+2^2+2^3+...+2^{2016}\)
\(A=2A-A=2^{2016}-2^0\)
\(A=2^{2016}-1\)
CM
3 tháng 9 2017
A = 3 − 1 + 3 + 1 ( 3 + 1 ) ( 3 − 1 ) + 2 ( 2 − 3 ) 2 = 2 3 3 − 1 + 2 − 3 = 3 + 2 − 3 = 2
H9
HT.Phong (9A5)
CTVHS
29 tháng 10 2023
Ta có: \(A=1+2+2^2+...+2^{2015}\)
\(2A=2\cdot\left(1+2+2^2+...+2^{2015}\right)\)
\(2A=2+2^2+2^3+...+2^{2016}\)
\(2A-A=2+2^2+...+2^{2016}-1-2-2^2-...-2^{2015}\)
\(A=2^{2016}-1\)
A không thể biết dưới dạng lũy thừa của 8 được
T
18 tháng 10 2023
a) \(A=2+2^2+2^3+...+2^{2017}\)
\(2A=2^2+2^3+2^4+...+2^{2018}\)
\(2A-A=\left(2^2+2^3+2^4+...+2^{2018}\right)-\left(2+2^2+2^3+...+2^{2017}\right)\)
\(A=2^{2018}-2\)
b) \(C=1+3^2+3^4+...+3^{2018}\)
\(3^2\cdot C=3^2+3^4+3^6+...+3^{2020}\)
\(9C-C=\left(3^2+3^4+3^6+...+3^{2020}\right)-\left(1+3^2+3^4+...+3^{2018}\right)\)
\(8C=3^{2020}-1\)
\(\Rightarrow C=\dfrac{3^{2020}-1}{8}\)
\(Toru\)
PT
1
CM
23 tháng 9 2018
a, P = 7 + 2 - 51 + 14 2 = 7 + 2 - 7 + 2 = 0
b, Q = 2 3 + 1 - 1 3 - 2 + 6 3 + 3
= 2 3 - 1 2 + 3 + 2 + 6 3 - 3 6
= 4 + 3
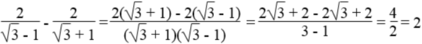
A = 1 + 1/22+1/23+...+1/22015
(1-1/2) A = (1-1/2) (1+1/22+1/23+...+1/22015) = 1 - 1/22016
A = 2 *( 1 -1/22016) = 2 -1/22015
A = 1 + 1/22+1/23+...+1/22015
(1-1/2) A = (1-1/2) (1+1/22+1/23+...+1/22015) = 1 - 1/22016
A = 2 *( 1 -1/22016) = 2 -1/22015