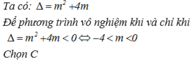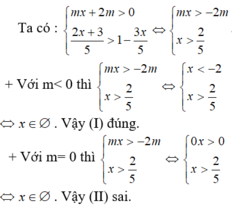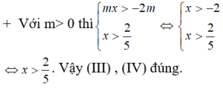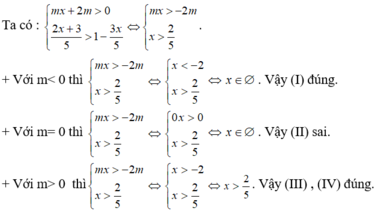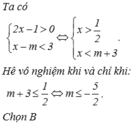Bất phương trình mx\(^2\)+2(m+3)x+m+1\(\ge\)0 vô nghiệm khi và chỉ khi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
27 tháng 5 2021
TH1: `m=0 `
`2x>0 <=> x>0`
`=>` Không thỏa mãn.
TH2: `m>0`
Bất PT có tập nghiệm là `RR <=> \Delta'<0`
`<=> (m-1)^2-m.4m<0`
`<=> m<-1 ; 1/3 <m`
Vậy `m in (0;+∞)` thỏa mãn.
27 tháng 5 2021
TH1 là m=0 thì TH2 là \(m\ne0\)
Bpt có tập nghiệm là R <=> \(\left\{{}\begin{matrix}a>0\\\Delta'< 0\end{matrix}\right.\)
Đáp án: m\(\in\left(\dfrac{1}{3};+\infty\right)\)
TD
3 tháng 2 2022
mx²+2(m-1)x+4 ≥0
bpt trên vô nghiệm <=>mx²+2(m-1)x+4 <0
a=m\(\ne0\)
\(\Delta'=\left(m-1\right)^2-m.4\)
\(=m^2-2m+1-4m\)
\(=m^2-6m+1\)
\(=\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)\)
bpt vô nghiệm <=>\(\left\{{}\begin{matrix}a< 0\\\Delta'< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\3-2\sqrt{2}< m< 3+2\sqrt{2}\end{matrix}\right.\)
=> không có m để bất phương trình vô nghiệm
CM
30 tháng 3 2017
Chọn A.
ĐK: 
TH1: m = 0: 
TH2:
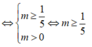
Vậy BPT đã cho vô nghiệm khi m ≥ 1 5
PT
1
CM
21 tháng 5 2019
Chọn A.
Với m = 0, bất phương trình trở thành 0.x < 3 + 0 ⇒ 0 > 3 (vô lý)
Bất phương trình vô nghiệm khi m = 0.
CM
25 tháng 4 2018
Ta có 2 x - 1 > 0 x - m < 3 ⇔ x > 1 2 x ≤ 3 + m .
Hệ vô nghiệm khi và chỉ khi: m + 3 ≤ 1 2 ⇔ x ≤ - 5 2 .