
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

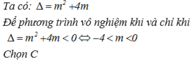

Để tam thức đổi dấu 2 lần
\(\Leftrightarrow x^2-\left(m+2\right)x+8m+1=0\) có 2 nghiệm pb
\(\Leftrightarrow\Delta=\left(m+2\right)^2-4\left(8m+1\right)>0\)
\(\Leftrightarrow m^2-28m>0\Rightarrow\left[{}\begin{matrix}m>28\\m< 0\end{matrix}\right.\)

Câu 1:
ĐKXĐ: x>=3
\(PT\Leftrightarrow\sqrt{x-3}=2x-m\)
=>x-3=(2x-m)^2
=>4x^2-4xm+m^2=x-3
=>4x^2-x(4m-1)+m^2+3=0
Δ=(4m-1)^2-4*4*(m^2+3)
=16m^2-8m+1-16m^2-48
=-8m-47
Để phương trình có nghiệm thì -8m-47>=0
=>m<=-47/8

Để (1) có 2 nghiệm thỏa mãn \(x_1< 2< x_2\)
\(\Leftrightarrow f\left(2\right)< 0\Leftrightarrow2^2-2.2-m< 0\)
\(\Leftrightarrow-m< 0\Rightarrow m>0\)

a)\(\left\{{}\begin{matrix}2m-1>0\Rightarrow m>\dfrac{1}{2}\left(1\right)\\m^2-\left(m-2\right)\left(2m-1\right)< 0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow m^2-\left(2m^2-m-4m+2\right)=-m^2+5m-2< 0\)
\(m^2-5m+2>0\Rightarrow\left[{}\begin{matrix}m< \dfrac{5-\sqrt{17}}{2}< \dfrac{1}{2}\\m>\dfrac{5+\sqrt{17}}{2}\end{matrix}\right.\)
Nghiệm hệ là
\(m>\dfrac{5+\sqrt{17}}{2}\)
b)\(\left\{{}\begin{matrix}m^2-m-2< 0\left(1\right)\\\left(2m-1\right)^2-4\left(m^2-m-2\right)\le0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\left(2m-1\right)^2-4\left(m^2-m-2\right)=9< 0,\forall m\).
Suy ra (2) vô nghiệm .
Kết luận hệ vô nghiệm.

Lười làm lắm cứ xét từng khoản là được
Đầu tiên giải bất thứ nhất
Ở bất thứ 2 xét 2 trường hợp
- TH 1: \(m\le0\)
- TH2: \(m>0\)
+ \(\hept{\begin{cases}m-x^2>0\\x+m< 0\end{cases}}\)
+\(\hept{\begin{cases}m-x^2< 0\\x+m>0\end{cases}}\)