Cho \(\Delta ABC\) thỏa mãn \(h_a=\sqrt{p\left(p-a\right)}\)
Chứng minh: \(\Delta ABC\) cân
ha là đường cao hạ từ đỉnh A
p là nửa chu vi tam giác
a là cạnh đối điện đỉnh A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 9 2023
Tham khảo:
Đặt \(a = BC,b = AC,c = AB\)
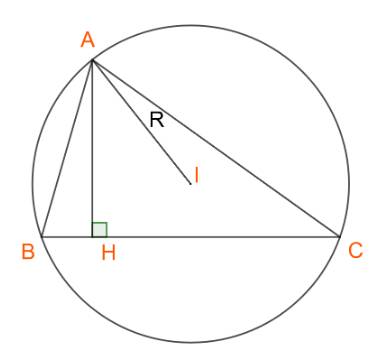
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)
AH
Akai Haruma
Giáo viên
22 tháng 2 2021
Lời giải:
Ta có: $S_{ABC}=\frac{h_a.a}{2}$
$S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$ theo công thức Heron.
$\Rightarrow \frac{h_a.a}{2}=\sqrt{p(p-a)(p-b)(p-c)}$
$\Leftrightarrow \frac{a\sqrt{p(p-a)}}{2}=\sqrt{p(p-a)(p-b)(p-c)}$
$\Leftrightarrow \frac{a}{2}=\sqrt{(p-b)(p-c)}$
$\Rightarrow \frac{a}{2}=\frac{1}{2}\sqrt{(a+c-b)(a+b-c)}$
$\Rightarrow a^2=(a+c-b)(a+b-c)$$\Leftrightarrow a^2=a^2-(b-c)^2\Rightarrow (b-c)^2=0$
$\Rightarrow b=c$ hay $ABC$ là tam giác cân.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 9 2016
+ Xét hai tg vuông BKC và tg vuông CHB có
Cạnh huyền BC chung (1)
\(S_{ABC}=\frac{AB.CK}{2}=\frac{AC.BH}{2}\) Mà AB=AC => BH=CK (2)
Từ (2) Và (2) => tg BKC = tg CHB (cạnh huyền và cạnh góc vuông tương ứng bằng nhau) => BK=CH (*)
Mà AB=AC=AK+BK=AH+CH => AK=AH => tg AKH cân tại A
+ Xét tg cân AKH có
^AKH=^AHK=(180-^BAC)/2 (3)
+ Xét tg cân ABC có
^ABC=^ACB=(180-^BAC)/2 (4)
Từ (3) và (4) => ^AKH=^ABC => KH//BC (có hai góc đồng vị bằng nhau) (**)
Từ (*) và (**) => BKHC là hình thang cân
7 tháng 4 2018
Ta có :
\(\left(a-b\right)^2\ge0\) ( với mọi độ dài a, b )
\(\left(b-c\right)^2\ge0\) ( với mọi độ dài b, c )
Mà \(\left(a-b\right)^2+\left(b-c\right)^2=0\)
\(\Rightarrow\)\(\hept{\begin{cases}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}a-b=0\\b-c=0\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}a=b\\b=c\end{cases}}\) ( chuyển vế )
Do đó :
\(a=b=c\)
Suy ra : tam giác ABC là tam giác đều
Vậy tam giác ABC là tam giác đều
Chúc bạn học tốt ~
HH
7 tháng 4 2018
Ta có \(\left(a-b\right)^2\ge0\)với mọi độ dài của a, b
và \(\left(b-c\right)^2\ge0\)với mọi độ dài của b, c
Mà \(\left(a-b\right)^2+\left(b-c\right)^2=0\)(gt)
=> \(\hept{\begin{cases}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\end{cases}}\)=> \(\hept{\begin{cases}a-b=0\\b-c=0\end{cases}}\)=> \(\hept{\begin{cases}a=b\\b=c\end{cases}}\)=> a = b = c
=> \(\Delta ABC\)đều (đpcm)
HQ
Hà Quang Minh
Giáo viên
13 tháng 1
a) Có AB ⊥ AC, HD ⊥ AB
=> HD // AC
=> \(\widehat {DHA} = \widehat {HAC}\)
- Xét tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \(\widehat {DHA} = \widehat {HAC}\)
=> ΔHDA ∽ ΔAHC
b) Xét tam giác ABC có: \(A{B^2} + A{C^2} = B{C^2}\)
mà AB=5cm, AC=4cm
=> \(BC = \sqrt {41} \)
- Có AH.BC=AB.AC
=> \(AH = \frac{{20\sqrt {41} }}{{41}}\)
=> \(H{B^2} = A{B^2} - A{H^2}\) (áp dụng định lý Pythagore trong tam giác vuông BHA)
=> \(HB = \frac{{25\sqrt {41} }}{{41}}\)
=> \(HC = \frac{{16\sqrt {41} }}{{41}}\)
- Xét tam giác vuông BDH và tam giác vuông BAC có: HD // AC
=> ΔBDH ∽ ΔBAC
=> \(\frac{{BH}}{{BC}} = \frac{{DH}}{{AC}}\)
=> \(H{\rm{D}} = \frac{{100}}{{41}}\)
\(S=\dfrac{1}{2}ah_a=\dfrac{1}{2}a\sqrt{p\left(b-a\right)}\) ; \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(\Rightarrow\dfrac{1}{2}a=\sqrt{\left(p-b\right)\left(p-c\right)}\)
\(\Leftrightarrow\dfrac{1}{2}a=\sqrt{\dfrac{\left(a+c-b\right)\left(a+b-c\right)}{4}}\Leftrightarrow a^2=\left(a+c-b\right)\left(a+b-c\right)\)
\(\Leftrightarrow b^2-2bc+c^2=0\Leftrightarrow\left(b-c\right)^2=0\)
\(\Leftrightarrow b=c\)