mng ơi cứu e vớiii !!!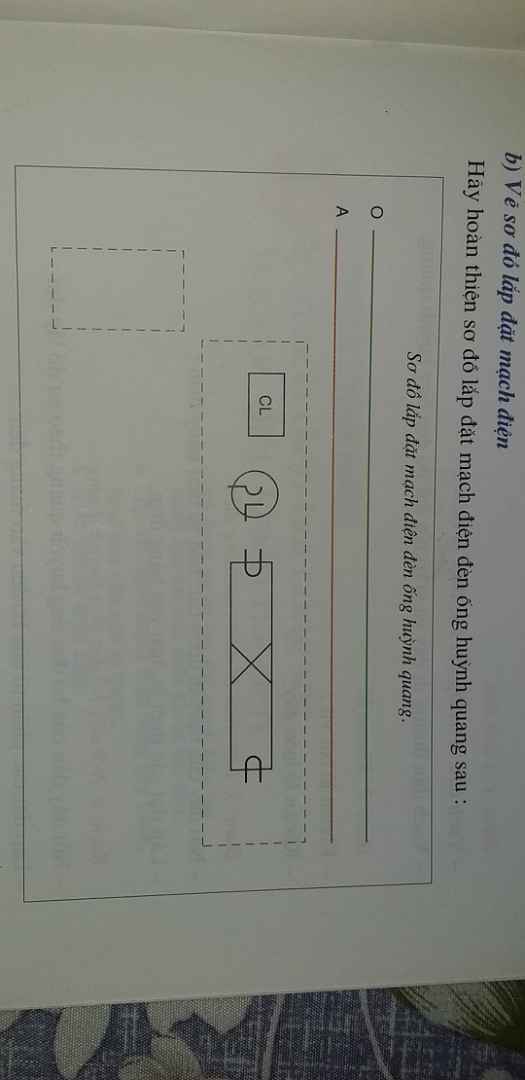
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Cách 1:
1. Chọn trang chiếu cần chèn hình ảnh vào;
2. Chọn lệnh Insert ⟶ Picture ⟶ From File. Hộp thoại Insert Picture xuất hiện. Xử lí hộp thoại
3. Chọn thư mục lưu tệp hình ảnh trong ô Look in
4. Nháy chọn tệp đồ họa cần thiết và nháy Insert.
Cách 2:
Lần lượt chọn các trang slide bên cột bên trái. Sử dụng lệnh Picture trong nhóm Images (trên dải lệnh Insert) để chèn hình ảnh thích hợp vào trang chiếu.

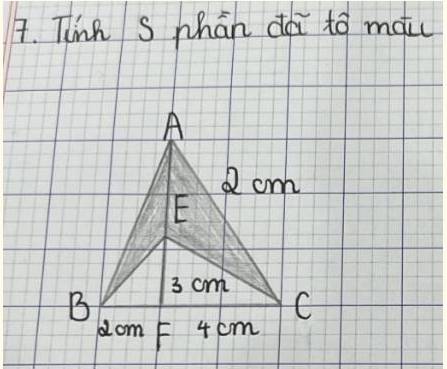
2cm là độ dàu của AE phải ko ạ?
độ dài đoạn BC là
4:2=6(cm)
diện tích tam giác EBC là
`3xx6:2=9(cm^2)`
độ dài đoạn AF là
`3+2=5(cm)`
diện tích tam giác ABC là
`5xx6:2=15(cm^2)`
diện tích phần tô đậm là
`15-9=6(cm^2)`
ds

\(n_{Fe}=\dfrac{1,68}{56}=0,03\left(mol\right)\)
PTHH: 3Fe + 2O2 ---to---> Fe3O4
0,03 0,02 0,01
V = VO2 = 0,02.24,79 = 0,4958 (l)
mFe3O4 = 0,01.232 = 2,32 (g)
PTHH: Fe3O4 + 4H2 ---to---> 3Fe + 4H2O
0,01 0,04
VH2 = 0,04.24,79 = 0,9916 (l)

\(2A+2nH_2SO_4\underrightarrow{to}A_2\left(SO_4\right)_n+nSO_2+2nH_2O\)

Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)

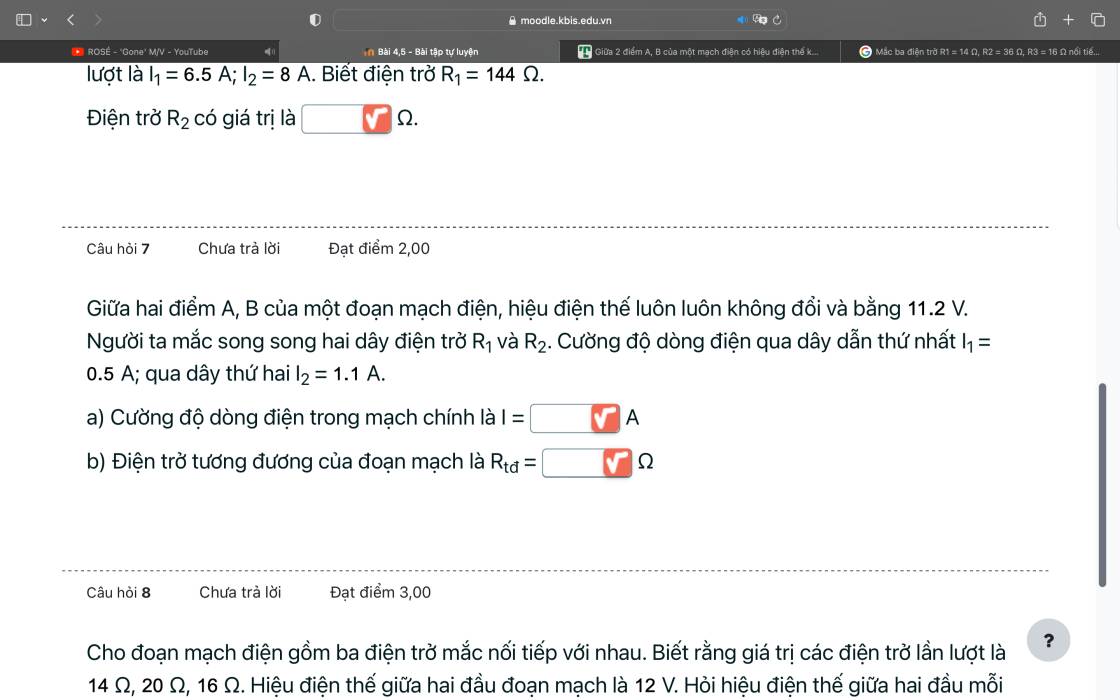
a: R1//R2
=>I=I1+I2=1,6(A)
b: R tđ=11,2/1,6=7(\(\Omega\))


3:
a: 5^n luôn có chữ số tận cùng là 5 với mọi n là số tự nhiên
=>5^100 có chữ số tận cùng là 5
b: \(2^{4k}\) có chữ số tận cùng là 6 với mọi k là số tự nhiên
mà 100=4*25
nên 2^100 có chữ số tận cùng là 6
c: 2023 chia 2 dư 1
mà \(9^{2k+1}\) luôn có chữ số tận cùng là 9
nên \(9^{2023}\) có chữ số tận cùng là 9
d: 2023 chia 4 dư 3
\(7^{4k+3}\left(k\in N\right)\) luôn có chữ số tận cùng là 3
Do đó: \(7^{2023}\) có chữ số tận cùng là 3
Quy luật:
+) các số có c/s tận cg là 0,1,5,6 nâng lên lũy thừa bậc nào (≠0) thì c/s tận cg vẫn là nó.
+) các số có tận cg là 2,4,8 nâng lên lt bậc 4n(n≠0) thì đều có c.s tận cg là 6.
+)các số có c/s tận cg là 3,7,9 nâng lên lt bậc 4n(n≠0) thì đều có c/s tận cg là 1.
+) số có tận cg là 3 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 7
+) số có tận cg là 7 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 3
+) số có tận cg là 2 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 8
+) số có tận cg là 8 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 2
+) số có c/s tận cg là 0,1,4,5,6,9 khi nâng lên lũy thừa bậc 4n+3 thì c/s tận cg là chính nó
Bài 3: áp dụng quy luật bên trên
\(a.5^{100}=\overline{..5}\)
\(b.2^{100}=2^{4.25}=\overline{..6}\)
\(c.9^{2023}=\overline{..9}\)
\(d.7^{2023}=7^{4.505+3}=\overline{...3}\)
Bài 4:
\(A=17^{2008}-11^{2008}-3^{2008}\)
\(=\left(\overline{...7}\right)^{4.502}-\left(\overline{..1}\right)^{2008}-\left(\overline{..3}\right)^{4.502}\)
\(=\overline{..1}-\overline{...1}-\overline{...1}\)
\(=\overline{..9}\)
Bài 5:
\(M=17^{25}+24^4-13^{21}\)
\(=\left(\overline{..7}\right)^{4.6}.\left(\overline{..7}\right)+\left(\overline{..4}\right)^{4.1}-\left(\overline{..3}\right)^{4.5}.\left(\overline{..3}\right)\)
\(\overline{..1}.\overline{..7}+\overline{..6}-\overline{..1}.\overline{..3}\)
\(=\overline{...7}+\overline{..6}-\overline{..3}\)
\(=\overline{...0}\)
\(=>M⋮10\)


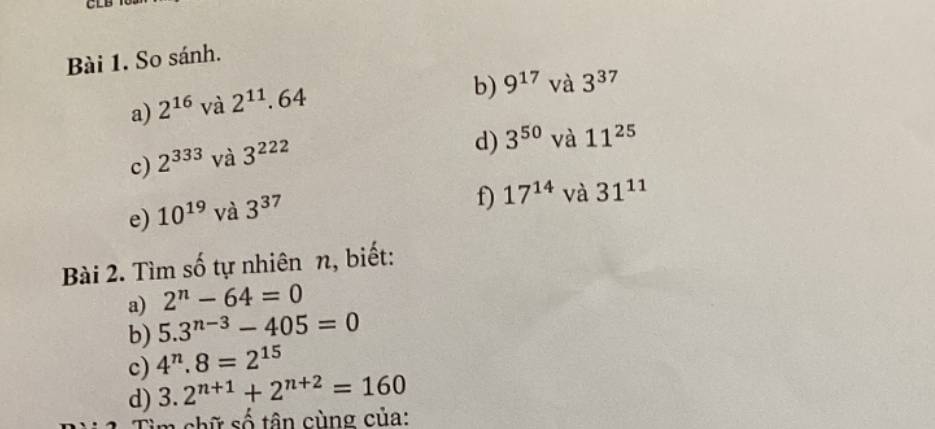

Nguồn: https://vietjack.com/giai-bai-tap-cong-nghe-9/ly-thuyet-thuc-hanh-lap-mach-dien-den-ong-huynh-quang.jsp