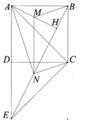
Cho hình vuông ABCD. Gọi điểm E là điểm đối xứng của A qua D
a) Chứng minh ∆ACE vuông cân
b) Từ A hạ AH vuông góc với BE. Chứng minh HD =AD
c) Gọi M, N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác
MNCB là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
16 tháng 10 2019
a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.
Þ D A C ^ = 450 Þ DACE vuông cân.
b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.
c) Do AH ^ BN, mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.
d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ A N C ^ = 900
a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông tại C