Cho 2 đường thẳng AB và CD cắt nhau tại I. Chứng minh: góc AIC= góc BID và góc AID= góc BIC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\widehat{BIC}\) và \(\widehat{BID}\) là hai góc kề bù:
\(\Rightarrow\widehat{BIC}+\widehat{BID}=180^o\)
Mà: \(BIC=\dfrac{2}{5}BID\)
\(\Rightarrow\widehat{BIC}=180^o:\left(2+5\right)\cdot2\approx51^o\)
\(\Rightarrow\widehat{BID}=180^o-\widehat{BIC}=180^o-51^o=129^o\)
Ta có: \(\widehat{AIC}\) đối đỉnh với \(\widehat{BID}\)
Và: \(\widehat{AID}\) đối đỉnh với \(\widehat{BIC}\)
\(\Rightarrow\widehat{AIC}=\widehat{BID}=129^o\)
\(\Rightarrow\widehat{AID}=\widehat{BIC}=51^o\)

a: \(\widehat{B}+\widehat{C}=130^0\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{130^0}{2}=65^0\)
hay \(\widehat{BIC}=115^0\)
b: Xét ΔDAI có \(\widehat{DAI}=\widehat{DIA}\)
nên ΔDAI cân tại D

a: \(\widehat{B}+\widehat{C}=130^0\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{130^0}{2}=65^0\)
hay \(\widehat{BIC}=115^0\)
b: Xét ΔDAI có \(\widehat{DAI}=\widehat{DIA}\)
nên ΔDAI cân tại D
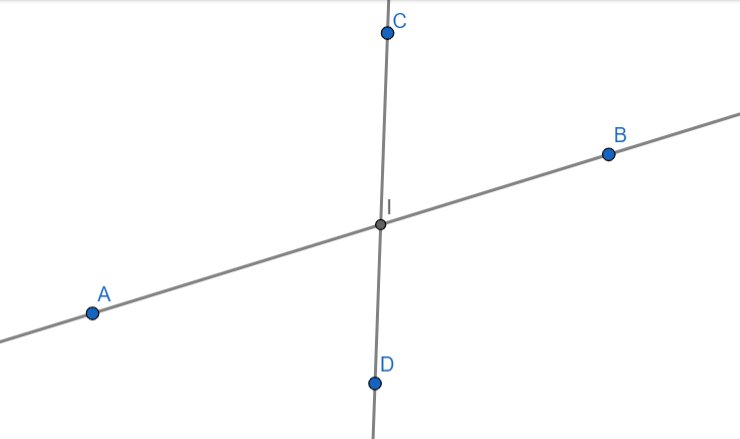

Bạn tự vẽ hình
Ta có:
AIC + AID = AID + DIB = 180 (2 góc kề bù)
Vậy AIC = DIB
Bạn làm tương tự