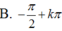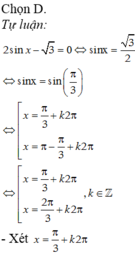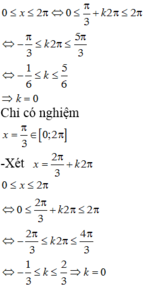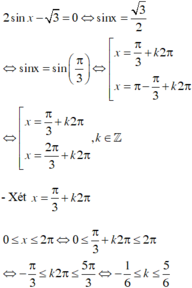2sinx -3=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2019
Đáp án:B.
Với f(x) = x 3 + 5x + 6 thì vì f'(x) = 3 x 2 + 5 > 0, ∀ x ∈ R nên hàm số f(x) luôn đồng biến trên R. Mặt khác f(-1) = 0. Vậy phương trình f(x) = 0 có nghiệm duy nhất trên R.
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2020
\(\Leftrightarrow\left(2sinx+1\right)\left(2sinx+1+sinx-\frac{3}{2}\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(3sinx-\frac{1}{2}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-\frac{1}{2}\\sinx=\frac{1}{6}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\\x=arcsin\left(\frac{1}{6}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{6}\right)+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2020
a/ \(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx-2=0\left(vn\right)\end{matrix}\right.\) (vô nghiệm do \(sinx\le1\) ; \(\forall x\))
\(\Leftrightarrow x=k\pi\)
b/ \(\Leftrightarrow\left[{}\begin{matrix}2sinx-3=0\\2sinx-\sqrt{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{3}{2}\left(vn\right)\\sinx=\frac{\sqrt{2}}{2}=sin\frac{\pi}{4}\end{matrix}\right.\) (lý do vô nghiệm như câu a)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{\pi}{4}+k2\pi\\sinx=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
c/ ĐKXĐ: \(sinx\ne-\frac{1}{2}\)
\(\Leftrightarrow2sinx-1=6sinx+3\)
\(\Leftrightarrow4sinx=-4\Rightarrow sinx=-1\)
\(\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
d/ \(\Leftrightarrow2=3-sinx\)
\(\Leftrightarrow sinx=1\Rightarrow x=\frac{\pi}{2}+k2\pi\)
(các câu \(k\in Z\) )
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2020
a/ \(sin^2x+sinx-3=m\)
Đặt \(sinx=t\Rightarrow-1\le t\le1\Rightarrow t^2+t-3=m\)
Xét \(f\left(t\right)=t^2+t-3\) trên \(\left[-1;1\right]\)
\(f\left(-1\right)=-3;\) \(f\left(1\right)=-1\) ; \(f\left(-\frac{1}{2}\right)=-\frac{13}{4}\)
\(\Rightarrow-\frac{13}{4}\le f\left(t\right)\le-1\)
\(\Rightarrow\) Để pt có nghiệm thì \(-\frac{13}{4}\le m\le-1\)
b/ Tương tự ta được \(-2\le m\le2\)
c/ \(\Leftrightarrow2cos^2x-1-cosx+m=0\)
\(\Leftrightarrow2t^2-t-1=-m\) với \(t=cosx\)
Giống câu a, ta được \(-\frac{9}{8}\le-m\le2\Rightarrow-2\le m\le\frac{9}{8}\)
d/\(\Leftrightarrow sinx=\frac{-2m+3}{2}\)
\(-1\le sinx\le1\Rightarrow-1\le\frac{-2m+3}{2}\le1\)
\(\Rightarrow\frac{1}{2}\le m\le\frac{5}{2}\)
DD
1
HP
15 tháng 8 2021
\(2sinx-\sqrt{3}=0\)
\(\Leftrightarrow sinx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(0\le\dfrac{\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{6}\le k\le\dfrac{5}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{\pi}{3}\)
\(0\le\dfrac{2\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{3}\le k\le\dfrac{4}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{2\pi}{3}\)
\(\Rightarrow x_1+x_2=\pi\)
PT
1
PT
1
NA
Giải pt:
\(\left(2sinx-1\right)^2-\left(2sinx-1\right)\left(sinx-\frac{3}{2}\right)=0\)
Giúp với ạ !
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2020
\(\Leftrightarrow\left(2sinx-1\right)\left(2sinx-1-sinx+\frac{3}{2}\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+\frac{1}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sinx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)