Trong mặt phẳng tọa độ, xét đường thẳng (d) : y= (m+1)x-4 với m =/=1. Tìm tất cả các giá trị của m để đường thẳng d cắt trục Ox và Oy lần lượt tại M và N sao cho tam giác OMN có diện tích bằng 4 (đvdt)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
(d’) tại điểm M. Gọi N và P lần lượt là giao điểm của đường thẳng (d) và (d’) với trục hoành Ox. Tìm m để diện tích tam giác OMP bằng 2 lần diện tích tam giác OMN.
CM
24 tháng 11 2019
Đáp án A
Ta có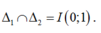 
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
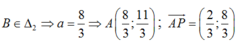
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0
22 tháng 5 2022
b: Tọa độ của điểm A là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}2x+2=x\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2\end{matrix}\right.\)
c: Gọi (d) là đường thẳng đi qua B(0;2) và song song với trục Ox
=>(d): y=2
Phương trình hoành độ giao điểm là:
x=2
=>y=2
Vậy: C(2;2)
d: A(-2;-2); B(0;2) C(2;2)
\(AB=\sqrt{\left(0+2\right)^2+\left(2+2\right)^2}=2\sqrt{5}\)
\(AC=\sqrt{\left(2+2\right)^2+\left(2+2\right)^2}=4\sqrt{2}\)
\(BC=\sqrt{\left(2-0\right)^2+\left(2-2\right)^2}=2\)
\(P=\dfrac{AB+AC+BC}{2}=\sqrt{5}+2\sqrt{2}+1\)
\(S=\sqrt{\left(\sqrt{5}+2\sqrt{2}+1\right)\left(\sqrt{5}-2\sqrt{2}+1\right)\left(\sqrt{5}+2\sqrt{2}-1\right)\left(-\sqrt{5}+2\sqrt{2}+1\right)}\)
\(=4\)