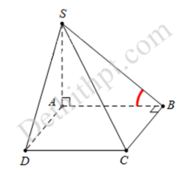
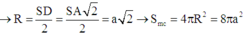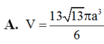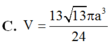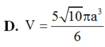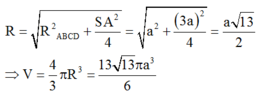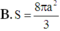Cho chóp S.ABCD đáy ABCD là hcn AB=2AD=2a, SA vuông góc với đáy, SC tạo với đáy một góc 30°. Tính Sxq chóp/S cầu ngoại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2017
Đáp án D
Theo định lí ba đường vuông góc ta có hai tam giác SBC và SDC lần lượt vuông góc tại B, D. Gọi I là trung điểm của SC thì ta có: IA = IB = ID = SC/2 = IS = IC nên I là tâm mặt cầu ngoại tiếp hình chóp. Bán kính mặt cầu ngoại tiếp hình chóp là 
CM
17 tháng 4 2019
Đáp án C
Từ giả thiết ta có SA ⊥ (ABCD), theo định lí ba đường vuông góc ta có tam giác SBC vuông tại B. Gọi S(B,r) là mặt cầu tâm B cắt SC theo một dây có độ dài 2a/3. Khi đó ta tính được:
15 tháng 12 2016
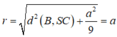
mình nghĩ câu hỏi của bạn chắc là nhầm thì phải.đáp án diện tích phải là:8π\(a^2\)
có phải bạn muốn tìm bán kính mặt cầu ngoại tiếp ko?nếu tìm bán kính ta làm như sau:SA=tan(60).AC=\(\sqrt{6}\)a
gọi O là tâm đáy suy ra AO=\(\frac{a\sqrt{2}}{2}\).từ O kẻ đt d vuông góc vs đáy .gọi Mlà trung điểm SA.trong mp(SAO) từ Mkẻ đt vuông góc SA cắt d tại I. I là tâm mặt cầu
R=IA=\(\sqrt{AI^2+AO^2}=a\sqrt{2}\)
CM
19 tháng 4 2017
Đáp án C
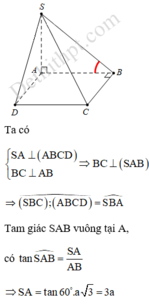
Do (SAB) ⊥ (ABCD) và (SAD) ⊥ (ABCD) ta có SA ⊥ (ABCD). Theo định lí ba đường vuông góc ta có BC ⊥ SB.
Hạ BH ⊥ SC tại H. Xét tam giác vuông SBC ta có:
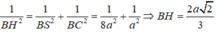
Ta có mặt cầu S(B;r) cắt đường thẳng SC theo một dây cung có độ dài 2a khi và chỉ khi ta có
CM
21 tháng 9 2019
Đáp án A
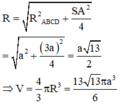
Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD là R A B C D = A C 2 = a
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABCD là
CM
21 tháng 2 2019
Đáp án A
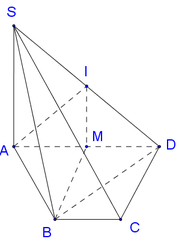
ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
