Có bao nhiêu giá trị nguyên của x, thỏa mãn: (x + 1).(x – 4) < 0
A. Vô số
B. 3
C. 0
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(x+2). (x+4) <0
TH1: (x+2) <0 và (x+4) >0
<=> x< -2 và x> -4
<=>x=3
TH2: (x+2) > 0 và (x+4)<0
<=> x> -2 và x< -4
Loại
=> Chỉ có 1 số thoả mãn là -3

tk
Ta có (x+3)(x+5)≥0(x+3)(x+5)≥0
Trường hợp 1: {x+3≥0x+5≥0{x+3≥0x+5≥0⇔{x≥−3x≥−5⇔{x≥−3x≥−5⇔x≥−3⇔x≥−3
Trường hợp 2: {x+3≤0x+5≤0{x+3≤0x+5≤0⇔{x≤−3x≤−5⇔{x≤−3x≤−5⇔x≤−5⇔x≤−5
Vậy để thỏa mãn (x+3)(x+5)≥0(x+3)(x+5)≥0 thì x≥−3x≥−3 hoặc x≤−5x≤−5
Suy ra có vô số số nguyên x
Đáp án B


a) A = \(\dfrac{1}{x-1}-\dfrac{4}{x+1}+\dfrac{8x}{\left(x-1\right)\left(x+1\right)}\)
= \(\dfrac{x+1-4x+4+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{5}{x-1}\) => đpcm
b) \(\left|x-2\right|=3=>\left[{}\begin{matrix}x-2=3< =>x=5\left(C\right)\\x-2=-3< =>x=-1\left(L\right)\end{matrix}\right.\)
Thay x = 5 vào A, ta có:
A = \(\dfrac{5}{5-1}=\dfrac{5}{4}\)
c) Để A nguyên <=> \(5⋮x-1\)
| x-1 | -5 | -1 | 1 | 5 |
| x | -4(C) | 0(C) | 2(C) | 6(C) |

Đáp án A
Ta có e 2 x + y + 1 - e 3 x + 2 y = x + y + 1 ⇔ e 2 x + y + 1 + 2 x + y + 1 = e 3 x + 2 y + 3 x + 2 y *
Xét f t = e t + t là hàm số đồng biến trên ℝ mà f 2 x + y + 1 = f 3 x + 2 y ⇒ y = 1 - x
Khi đó log 2 2 2 x + y - 1 - m + 4 log 2 x + m 2 + 4 = 0
Phương trình (1) có nghiệm khi và chỉ khi ∆ = m + 4 - 4 m 2 + 4 ≥ 0 ⇔ 0 ≤ m ≤ 8 3 .

Ta có \(\left(x+3\right)\left(x+5\right)\ge0\)
Trường hợp 1: \(\left\{{}\begin{matrix}x+3\ge0\\x+5\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\x\ge-5\end{matrix}\right.\)\(\Leftrightarrow x\ge-3\)
Trường hợp 2: \(\left\{{}\begin{matrix}x+3\le0\\x+5\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le-3\\x\le-5\end{matrix}\right.\)\(\Leftrightarrow x\le-5\)
Vậy để thỏa mãn \(\left(x+3\right)\left(x+5\right)\ge0\) thì \(x\ge-3\) hoặc \(x\le-5\)
Suy ra có vô số số nguyên x
Đáp án B

Chọn đáp án B
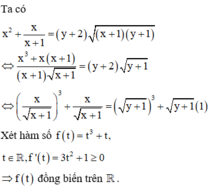
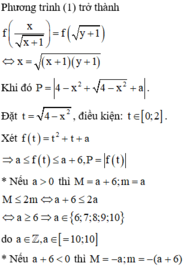
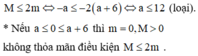
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
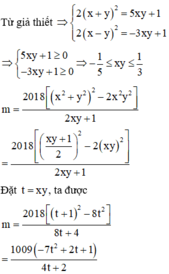
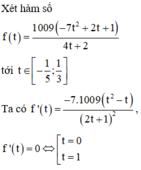
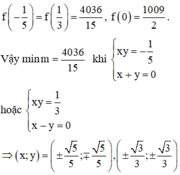
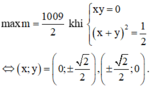
Chọn D
D