tập nghiệm của bất phương trình (x-1)(x+3)\(\ge\)0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(2x + 3 \ge 0 \Leftrightarrow x \ge \frac{{ - 3}}{2}\)
\( \Rightarrow \) Tập hợp E là: \(E = \left\{ {x \in \mathbb{R}|x \ge \frac{{ - 3}}{2}} \right\}\)
và \( - x + 5 \ge 0 \Leftrightarrow x \le 5\)
\( \Rightarrow \) Tập hợp G là \(G = \left\{ {x \in \mathbb{R}|x \le 5} \right\}\)
\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x \ge \frac{{ - 3}}{2}\) và \(x \le 5\)} \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\}\)
Vậy tập hợp D \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\} = [\frac{{ - 3}}{2}; 5]\)
b) Ta có: \(x + 2 > 0 \Leftrightarrow x>-2\)
\( \Rightarrow E = \left\{ {x \in \mathbb{R}|x >-2 }\right\}\)
và \( 2x - 9 < 0 \Leftrightarrow x < \frac{9}{2}\)
\( \Rightarrow G = \left\{ {x \in \mathbb{R}|x < \frac{9}{2}} \right\}\)
\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x > -2 \) và \(x < \frac{9}{2}\)} \( = \left\{ {x \in \mathbb{R}|-2<x< {9\over 2} } \right\}\)
Vậy \( D= \left\{ {x \in \mathbb{R}|-2<x< {9\over 2}} \right\}=(-2;{9\over 2})\)

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn


\(\Leftrightarrow\left(2x-3\right)\left(2x+7\right)< =0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+7>=0\\2x-3< =0\end{matrix}\right.\Leftrightarrow-\dfrac{7}{2}< =x< =\dfrac{3}{2}\)

- Với \(m=\dfrac{1}{2}\Rightarrow\left(x+1\right)^2>0\) có tập nghiệm \(R\backslash\left\{-1\right\}\) thỏa mãn
- Với \(m>\dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-1\\x< -2m\end{matrix}\right.\) hay \(D=\left(-\infty;-2m\right)\cup\left(-1;+\infty\right)\)
Thỏa mãn do \(\left(1;+\infty\right)\subset\left(-1;+\infty\right)\)
- Với \(m< \dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-2m\\x< -1\end{matrix}\right.\) hay \(D=\left(-\infty;-1\right)\cup\left(-2m;+\infty\right)\)
Tập nghiệm của BPT chứa \(\left(1;+\infty\right)\) khi:
\(-2m\le1\Rightarrow m\ge-\dfrac{1}{2}\Rightarrow-\dfrac{1}{2}\le m< \dfrac{1}{2}\)
Kết hợp lại ta được: \(m\ge-\dfrac{1}{2}\)

Tham khảo:
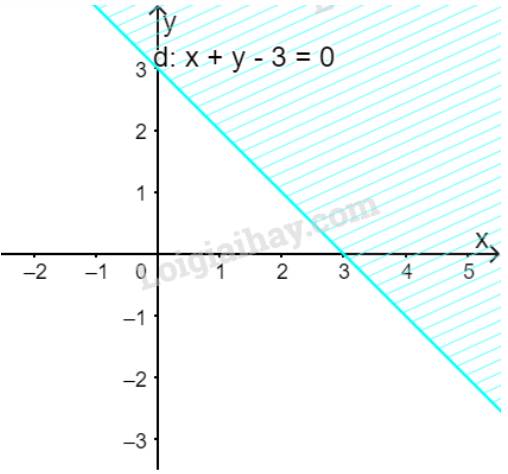
Vẽ đường thẳng \(d:x + y - 3 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 0 - 3 = - 3 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(d\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Vẽ đường thẳng \(d': - 2x + y + 3 = 0\) đi qua hai điểm \(A(1; - 1)\) và \(B\left( {2;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 + 3 = 3 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
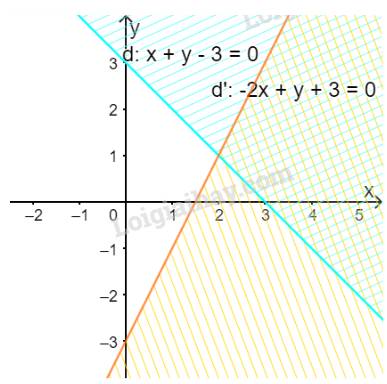
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.

Đáp án: B
Ta có:
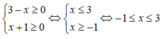
Vậy tập nghiệm của hệ bất phương trình là: [-1;3]

Ta có: \(x-1=0\Rightarrow x=1\),\(x+3=0 \Rightarrow x = - 3\)
BXD:
Vậy \(T=(-\infty;-3]\cup[1;+\infty)\)
- Đặt \(f\left(x\right)=\left(x-1\right)\left(x+3\right)\)
- Cho \(f\left(x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
- Lập bảng xét dấu :
x___________-3_________________1______________
x-1____-_____|________-_________0______+___________
x+3___-______0_______+_________|_____+____________
f(x)___+______0_______-__________0_____+____________
- Từ bảng xét dấu :- Để f(x) \(\ge0\)
Vậy phương trình có tập nghiệm \((-\infty;-3]\cup[1;+\infty)\)