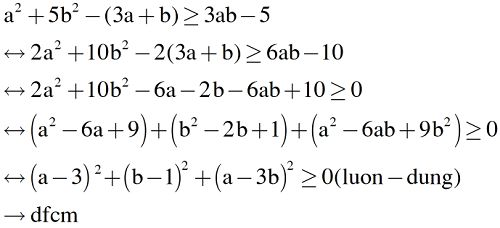Chứng minh a2 + 5b2-(3a+b)>= 3ab-5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2018
Links:
Chứng minh $a^2+5b^2-(3a+b)\geq 3ab-5$ - Bất đẳng thức và cực trị - Diễn đàn Toán học
Chứng minh a^2 + 5b^2 - (3a + b) ≥ 3ab - 5 - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
8 tháng 8 2021
Ta có: \(VP=\left(a-b\right)\left(a^2+ab+b^2\right)-3ab\left(a-b\right)\)
\(=a^3-b^3-3a^2b+3ab^2\)
\(=a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3=VT\)
⇒ đpcm
8 tháng 8 2021
\(\left(a-b\right)\left(a^2+ab+b^2\right)-3ab\left(a-b\right)\)
\(=\left(a-b\right)\left(a^2+ab+b^2-3ab\right)\)
\(=\left(a-b\right)^3\)
14 tháng 5 2021
a )
`VP= (a+b)^3-3ab(a+b)`
`=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2`
`=a^3+b^3 =VT (đpcm)`
b)
b) Ta có
`VT=a3+b3+c3−3abc`
`=(a+b)3−3ab(a+b)+c3−3abc`
`=[(a+b)3+c3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)2+c2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a2+b2+2ab+c2−ac−bc−3ab)`
`=(a+b+c)(a2+b2+c2−ab−bc−ca)=VP`
14 tháng 5 2021
a) Ta có:
`VP= (a+b)^3-3ab(a+b)`
`=a^3 + b^3+3ab ( a + b )- 3ab ( a + b )`
`=a^3 + b^3=VT(dpcm)`
b) Ta có
`VT=a^3+b^3+c^3−3abc`
`=(a+b)^3−3ab(a+b)+c^3−3abc`
`=[(a+b)^3+c^3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)^2+c^2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a^2+b^2+2ab+c^2−ac−bc−3ab)`
`=(a+b+c)(a^2+b^2+c^2−ab−bc−ca)=VP`
2 tháng 5 2020
Bài làm
Ta có: 3a3 + 3a2b + 3ab2 + 3b3
= 3( a3 + a2b + ab2 + b3 )
= 3[ a2( a + b ) + b2( a + b ) ]
= 3( a2 + b2 )( a + b )
Ta có: ( a2 + b2 ) > 0 V a, b
=> ( a2 + b2 ) . 3 > 0
Mà 3( a2 + b )2( a + b ) > 0 ( đpcm )
2 tháng 5 2020
\(3a^3+3a^2b+3ab^2+3b^3>0\)
\(\Leftrightarrow3\left(a^3+a^2b+ab^2+b^3\right)>0\)
\(\Leftrightarrow3\left[a^2\left(a+b\right)+b^2\left(a+b\right)\right]>0\)
\(\Leftrightarrow3\left(a^2+b^2\right)\left(a+b\right)>0\)(đpcm)
AT
2
H9
HT.Phong (9A5)
CTVHS
27 tháng 7 2023
1) \(\left(a+b\right)^2\)
\(=\left(a+b\right)\left(a+b\right)\)
\(=a^2+ab+ab+b^2\)
\(=a^2+2ab+b^2\left(dpcm\right)\)
2) \(\left(a-b\right)^3\)
\(=\left(a-b\right)\left(a-b\right)\left(a-b\right)\)
\(=\left(a^2-ab-ab+b^2\right)\left(a-b\right)\)
\(=\left(a^2-2ab+b^2\right)\left(a-b\right)\)
\(=a^3-a^2b-2a^2+2ab^2+ab^2-b^3\)
\(=a^3-3a^2b+3ab^2-b^3\left(dpcm\right)\)
C
3
C
1
28 tháng 7 2021
a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)
\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)
\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)
Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)