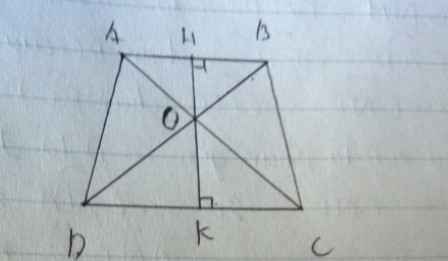
Cho hình thang ABCD, đáy lớn là DC, đáy nhỏ là AB. Hai đường chéo cắt nhau tại O . So sánh diện tích hai tam giác AOD và BOC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 4
Vì AB//CD
nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
Ta có: \(\dfrac{S_{BOA}}{S_{BOC}}=\dfrac{OA}{OC}\)
\(\dfrac{S_{BOA}}{S_{AOD}}=\dfrac{OB}{OD}\)
mà \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
nên \(S_{BOC}=S_{AOD}\)
NB
27 tháng 6 2021
\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
31 tháng 8 2020
Ta có: AB // CD => góc ABD = góc BDC (slt) và góc BAC = góc ACD
Xét tam giác OAD và tam giác OAB và tam giác OCD có:
ABD=BDC (Cmt)
BAC=ACD (cmt)
=> tam giác OAD đồng dạng với tam giác OAB
=> OA/OC = OB/OD
=> OA.OD =OB.OC (đpcm)
18 tháng 1 2016
a) 2 tam giác ABC và BCD có cùng đường cao là đường cao = đương cao hình thang đáy DC = 2AB --> diện tich BCD gấp đôi
b) dễ dàng cm được diện tích tam giác diện tích tam giác ADC = BDC chúng có phần chung DOC còn lại phần riêng AOD = BOC
mày là thằng nào .............