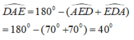Cho tam giác ABC vuông tại A . Trên cạnh BC lấy điểm D và E sao cho BD=BA và CE=CA . Tính góc DAE?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GP
1
26 tháng 12 2018
ΔABD cân tại B có 
ΔACE cân tại C có 
TQ
0
10 tháng 1 2020
Hình tự vẽ ..
Giair
Vì AB=BD => \(\Delta ABD\)cân tại B
\(\Rightarrow\widehat{ADB}=\frac{180^0-\widehat{B}}{2}\)
vì CE=CA => \(\Delta AEC\)cân tại C
\(\Rightarrow\widehat{AEC}=\frac{180^0-\widehat{C}}{2}\)
Do đó : \(\widehat{ADB}+\widehat{AEC}=\frac{360^0-\widehat{B}-\widehat{C}}{2}=\frac{360^0-90^0}{2}=\frac{270^0}{2}=135^0\)
\(\Rightarrow90^0+\widehat{DAE}=135^0\)
\(\Rightarrow\widehat{DAE}=135^0-90^0\)
\(\Rightarrow\widehat{DAE}=45^0\)
PM
Trên cạnh huyền BC của tam giác vuông ABC , lấy các điểm D và E sao cho BD=BA , CE=CA. Tính góc DAE.
4
26 tháng 12 2018
ΔABD cân tại B có
ΔACE cân tại C có
YN
26 tháng 12 2021
Answer:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow100^o+\widehat{C}+\widehat{B}=180^o\)
\(\Rightarrow2\widehat{B}=80^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=40^o\)
Ta có: Tam giác ACE cân tại C
Mà: \(\widehat{A}+\widehat{C}+\widehat{E}=180^o\)
\(\Rightarrow2\widehat{E}+40^o=180^o\)
\(\Rightarrow2\widehat{E}=140^o\)
\(\Rightarrow\widehat{E}=70^o\) (1)
Ta có: Tam giác ABD cân tại B
Mà: \(\widehat{A}+\widehat{B}+\widehat{D}=180^o\)
\(\Rightarrow2\widehat{D}+40^o=180^o\)
\(\Rightarrow2\widehat{D}=140^o\)
\(\Rightarrow\widehat{D}=70^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{A}+\widehat{E}+\widehat{D}=180^o\)
\(\Rightarrow\widehat{A}+2.70^o=180^o\)
\(\Rightarrow\widehat{A}+140^o=180^o\)
\(\Rightarrow\widehat{A}=40^o\)
Vậy \(\widehat{DAE}=40^o\)
26 tháng 12 2018
ΔABD cân tại B có
ΔACE cân tại C có
CM
30 tháng 7 2018
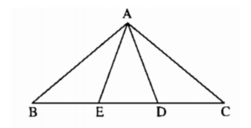
+) Ta có:
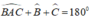(tổng ba góc trong 1 tam giác)
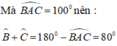
Lại có: tam giác ABC là tam giác cân tại A nên:
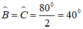
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.
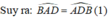
Lại có;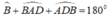 
( tổng ba góc trong 1 tam giác)
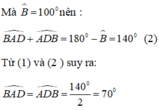
+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)
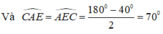
+) Xét tam giác ADE có:
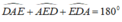( tổng ba góc trong tam giác)
Suy ra:
