Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
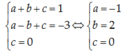
Vậy (P): y = -x2 + 2x
Chọn C.

(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.

+ Parabol y = ax2 + bx + c đi qua điểm A (8; 0)
⇒ 0 = a.82 + b.8 + c ⇒ 64a + 8b + c = 0 (1).
+ Parabol y = ax2 + bx + c có đỉnh là I (6 ; –12) suy ra:
–b/2a = 6 ⇒ b = –12a (2).
–Δ/4a = –12 ⇒ Δ = 48a ⇒ b2 – 4ac = 48a (3) .
Thay (2) vào (1) ta có: 64a – 96a + c = 0 ⇒ c = 32a.
Thay b = –12a và c = 32a vào (3) ta được:
(–12a)2 – 4a.32a = 48a
⇒ 144a2 – 128a2 = 48a
⇒ 16a2 = 48a
⇒ a = 3 (vì a ≠ 0).
Từ a = 3 ⇒ b = –36 và c = 96.
Vậy a = 3; b = –36 và c = 96.

(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình 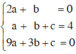
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.

Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\-\dfrac{b^2-4ac}{4a}=1\\16a+4b+c=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\16a^2-4ac=-4a\\16a-16b+c=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=5\\16a^2+4a-20=0\\b=-4a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=5\\16a^2+20a-16a-20=0\\b=-4a\end{matrix}\right.\)
Đến đây bạn tự làm tiếp được rồi

THam khảo
Bài 2:
Ta có: −Δ4a=−3−Δ4a=−3
⇔−Δ=−12a⇔−Δ=−12a
⇔b2−4a=12a⇔b2−4a=12a
⇔b2−16a=0(1)⇔b2−16a=0(1)
Thay x=-1 và y=6 vào (P), ta được:
a⋅(−1)2+b(−1)+1=6a⋅(−1)2+b(−1)+1=6
⇔a−b=5⇔a−b=5
⇔a=b+5⇔a=b+5(2)
Thay (2) vào (1), ta được:
b2−16(b+5)=0b2−16(b+5)=0
⇔b2−16b+64−144=0⇔b2−16b+64−144=0
⇔(b−8)2=144⇔(b−8)2=144
⇔[b=20b=−4⇔[a=25a=1

1/ Do (P) qua A \(\Rightarrow c=1\) (thay tọa độ A vào pt (P) thôi)
(P) có đỉnh nằm trên trục hoành
\(\Rightarrow-\frac{\Delta}{4a}=0\Rightarrow\Delta=0\Rightarrow b^2-4ac=0\Rightarrow b^2=4ac=4a\Rightarrow a=\frac{b^2}{4}\)
Do (P) qua B \(\Rightarrow4a+2b+c=1\Rightarrow b^2+2b=0\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow a=0\left(l\right)\\b=-2\Rightarrow a=1\end{matrix}\right.\)
2/ Cần tìm 3 ẩn mà chỉ cho 1 dữ liệu, how to giải?
3/ \(-\frac{b}{2a}=2>1>-2\) và \(a=1>0\)
\(\Rightarrow\) hàm số nghịch biến trên \(\left[-2;1\right]\)
\(\Rightarrow y_{max}=y\left(-2\right)=15\)
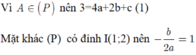
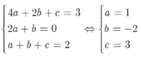
Do (p) đi qua A(0;3), B(3;0) và C(-1;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3=c\\9a+3b+c=0\\a+b+c=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}c=3\\3a+b=-1\\a+b=-4\end{matrix}\right.\\ \Leftrightarrow \left\{{}\begin{matrix}c=3\\a=\dfrac{3}{2}\\b=\dfrac{-11}{2}\end{matrix}\right.\)