
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì (P) đi qua M(4;3) nên 3= 16a+ 4b+c (1)
Mặt khác (P) cắt Ox tại N(3;0) suy ra 0=9a+3b+c (2) , (P) cắt Ox tại P nên P(t; 0) với 0= at2+ bt+c (*) ; (P) cắt Ox tại N và P nên phương trình (*) có 1 nghiệm là t=3 ( hoành độ điểm N)

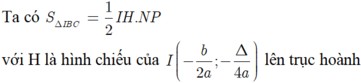
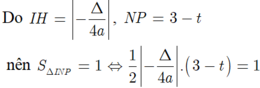
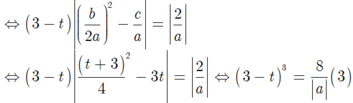
Từ (1) và (2); vế trừ vế ta có 7a+ b=3 hay b= 3-7a
suy ra: 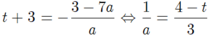
Thay vào (3) ta có:
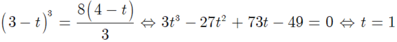
Suy ra a= 1; b= -4; c=3.
Vậy (P) cần tìm là y= x2-4x+3.
Chọn B.

Lời giải:
$(P)$ đi qua đi qua $A(0;3), B(-1;4)$ khi mà:
\(\left\{\begin{matrix} y_A=4x_A^2+bx_A+c\\ y_B=4x_B^2+bx_B+c\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3=4.0^2+b.0+c\\ 4=4.(-1)^2+b(-1)+c\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} c=3\\ -b+c=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} c=3\\ b=3\end{matrix}\right.\)
Vậy $(P): y=4x^2+3x+3$


(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.

\(ĐK:a\ne0\)
\(A\left(0;1\right)\in\left(P\right)\Leftrightarrow c=1\)
(P) có đỉnh trên trục hoành \(\Leftrightarrow\Delta=b^2-4ac=0\Leftrightarrow b^2=4ac=4a\Leftrightarrow a=\dfrac{b^2}{4}\)
\(B\left(2;1\right)\in\left(P\right)\Leftrightarrow4a+2b+c=1\\ \Leftrightarrow b^2+2b=0\\ \Leftrightarrow\left[{}\begin{matrix}b=0\Leftrightarrow a=0\left(ktm\right)\\b=-2\Leftrightarrow a=1\left(tm\right)\end{matrix}\right.\)
Vậy \(a+b+c=1-2+1=0\)

+ Parabol y = ax2 + bx + c đi qua điểm A (8; 0)
⇒ 0 = a.82 + b.8 + c ⇒ 64a + 8b + c = 0 (1).
+ Parabol y = ax2 + bx + c có đỉnh là I (6 ; –12) suy ra:
–b/2a = 6 ⇒ b = –12a (2).
–Δ/4a = –12 ⇒ Δ = 48a ⇒ b2 – 4ac = 48a (3) .
Thay (2) vào (1) ta có: 64a – 96a + c = 0 ⇒ c = 32a.
Thay b = –12a và c = 32a vào (3) ta được:
(–12a)2 – 4a.32a = 48a
⇒ 144a2 – 128a2 = 48a
⇒ 16a2 = 48a
⇒ a = 3 (vì a ≠ 0).
Từ a = 3 ⇒ b = –36 và c = 96.
Vậy a = 3; b = –36 và c = 96.
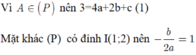
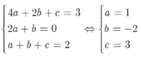
Do (p) đi qua A(0;3), B(3;0) và C(-1;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3=c\\9a+3b+c=0\\a+b+c=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}c=3\\3a+b=-1\\a+b=-4\end{matrix}\right.\\ \Leftrightarrow \left\{{}\begin{matrix}c=3\\a=\dfrac{3}{2}\\b=\dfrac{-11}{2}\end{matrix}\right.\)