Trong không gian Oxyz, đường thẳng d : x − 3 1 = y + 2 − 1 = z − 4 2 cắt mặt phẳng O x y tại điểm có tọa độ là:
A. − 3 ; 2 ; 0
B. 3 ; − 2 ; 0
C. − 1 ; 0 ; 0
D. 1 ; 0 ; 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)

Chọn A
Mặt phẳng (P) có vectơ pháp tuyến là n → =(1;1;1)
Gọi ∆ là đường thẳng cần tìm và
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
![]()
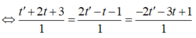
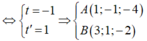

Đáp án D
Phương pháp:
+) Gọi M là giao điểm của đường thẳng d và mặt phẳng (Oxy). Khi đó tọa độ điểm M thỏa mãn phương trình đường thẳng d và mặt phẳng (Oxy).
+) Phương trình mặt phẳng (Oxy): z=0
Cách giải:
Gọi M x 0 ; y 0 ; z 0 là giao điểm của đường thẳng d và mặt phẳng (Oxy): z 0 = 0
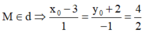
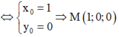
Đáp án D
M ∈ d ⇒ x 0 − 3 1 = y 0 + 2 − 1 = 4 2 ⇔ x 0 = 1 y 0 = 0 ⇒ M 1 ; 0 ; 0