Cho lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác vuông tại B, đường cao BH. Biết A ' H ⊥ A B C v à A B = 1 , A C = 2 , A A ' = 2 Thể tích của khối lăng trụ đã cho bằng
A. 21 12
B. 7 4
C. 21 4
D. 3 7 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

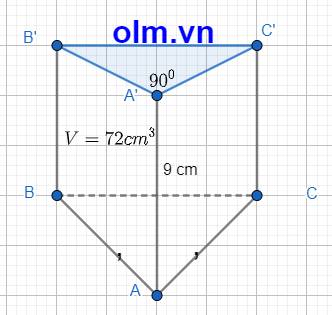
VABCA'B'C' = SABC.h
Diện tích của tam giác ABC là: 72 : 9 = 8 (cm2)
SABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB2 = 8 ⇒ AB2 = 8.2 = 16
⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)
Vậy độ dài cạnh đáy AB dài 4cm

Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:
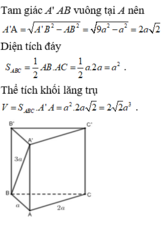
Phương pháp:
Thể tích khối lăng trụ có chiều cao h và diện tích đáy S là V = h.S
Tính toán các cạnh dựa vào định lý Pytago và hệ thức lượng trong tam giác vuông.
Cách giải:
Xét tam giác vuông ABC có: