cho đường tròn tâm O và điểm A ở ngoài đường tròn.Vẽ 2 tiếp tuyến AB,AC(B,C là 2 tiếp điểm),AO cắt đường tròn tại I và K(I nằm giữa A và K).a)Chứng minh AO vuông góc BC tại H.b)Chứng minh :BI là phân giác góc ABC.c)Chứng minh :AB mũ 2 =AI nhân AK d)Chứng minh :AI.KH=AK.IH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 7 2018
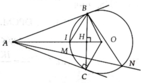
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC
11 tháng 11 2021
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trực của BC
hay OA⊥BC
27 tháng 1 2022
a; Xét ΔOBD có OB=OD
nên ΔOBD cân tại O
Suy ra: \(\widehat{DBO}=\widehat{ODB}\)
mà \(\widehat{ODB}=\widehat{ABC}\)
nên \(\widehat{DBO}=\widehat{ABC}\)
26 tháng 12 2021
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm tren đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC