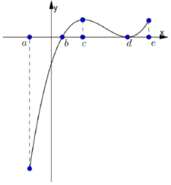
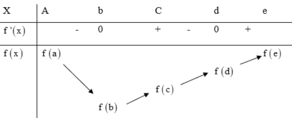
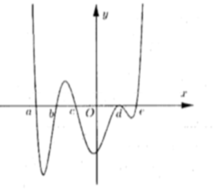
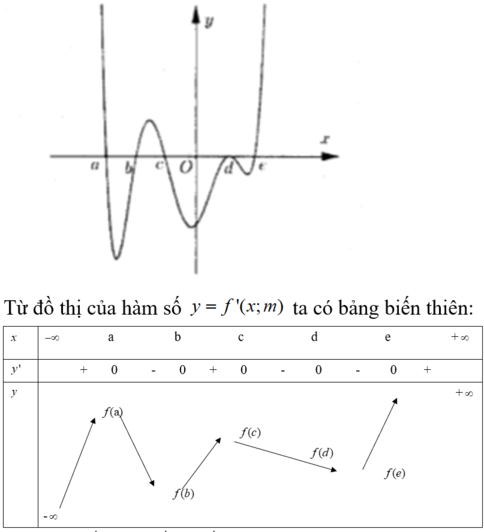
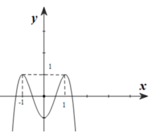
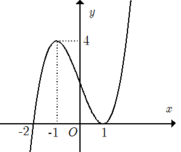
Cho hàm số f x = a x 4 + b x 3 + c x 3 + d x + e a ≠ 0 . Biết rằng hàm số f(x) có đạo hàm là f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?
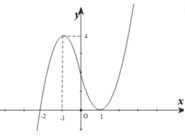
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)
B. Hàm số f(x) đồng biến trên khoảng 0 ; + ∞
C. Hàm số f(x) đồng biến trên khoảng (-2;1)
D. Hàm số f(x) nghịch biến trên khoảng - ∞ ; - 2