Cho một nửa đường tròn đường kính AB. Điểm M chạy trên nửa đường tròn. Kẻ MH vuông góc với AB tại H. Đặt MH = x. Khi M chuyển động thì x thay đổi, do đó tích AH.BH cũng thay đổi theo. Kí hiệu tích AH.BH bởi P(x). Hỏi P(x) có phải là một hàm số của biến số x hay không? Viết công thức biểu thị hàm số này..
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 1 2018
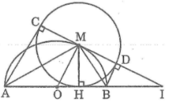
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 11 2023
a/
Ta có \(\widehat{AMB}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông AMB có
\(MH^2=AH.BH\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền = tích giữa các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow BH=\dfrac{MH^2}{AH}=\dfrac{4^2}{2}=8cm\)
\(\Rightarrow AB=AH+BH=2+8=10cm\)
\(MA^2=AH.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow MA=\sqrt{AH.AB}=\sqrt{2.10}=2\sqrt{5}cm\)
\(MB^2=BH.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow MB=\sqrt{BH.AB}=\sqrt{8.10}=4\sqrt{5}cm\)
b/ Không rõ bạn hỏi biểu thức nào?
c/
Ta có \(OD\perp AM\) (2 tiếp tuyến cùng xuất phát từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm đường tròn vuông góc với dây cung nối 2 tiếp điểm)
Xét tg vuông AIO
Gọi K là trung điểm của AO => AK=OK
\(\Rightarrow IK=AK=OK=\dfrac{1}{2}AO\) không đổi (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Ta có
A; O cố định => K cố định; IK không đổi => khi M di chuyển trên nửa (O) => I chạy trên nửa đường tròn tâm K
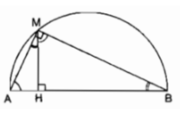
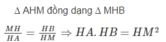
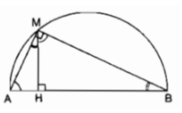
Với mỗi giá trị của x ta có một giá trị xác định của P(x).
Vậy P(x) là một hàm số.
P(x) = x 2