Cho hàm số y = 0,2 x 2
Biết rằng điểm C(c ; 6) thuộc đồ thị, hãy tính c. Điểm D(c ; -6) có thuộc đồ thị hàm số không ? Vì sao ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số y = 0,2 x 2 đi qua điểm A(-2 ; b) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có : b = 0,2. - 2 2 = 0,8
Điểm A(-2; b) thuộc đồ thị hàm số y = 0,2 x 2 mà điểm A’(2 ; b) đối xứng với điểm A(-2; b) qua trục tung nên điểm A’(2; b) thuộc đồ thị hàm số y = 0,2 x 2

tội nghiệt bạn giữa cái bài từ hôm qua tới giờ mà chưa ai giải

+ Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’ (x) là parabol có trục đối xứng là trục tung nên b=0
Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.
Suy ra: f’(x) = 3x2-3b và f(x) = x3-3x+d.
+ Do (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm nên ta có:
f’(x) =0 khi và chỉ khi x= -1;x= 1( loại)
Như vậy (C) đi qua điểm (-1; 4) ta tìm được d= 2
Khi đó; f( x) =x3-3x+2.
chọn A.

\(f\left(0\right)=5=>c=5;f\left(2\right)=4.a+2.b+5=0;f\left(5\right)=25a+5b+5=0\Leftrightarrow5a+b+1=0\)
\(\hept{\begin{cases}4a+2b+5=0\\5a+b+1=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}4a+2b+5=0\\10a+2b+2=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}4a+2b+5=0\\6a-3=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=-\frac{7}{2}\\a=\frac{1}{2}\end{cases}}\)
\(f\left(x\right)=\frac{1}{2}x^2-\frac{7}{2}x+5\)
b)
\(f\left(-1\right)=\frac{1}{2}+\frac{7}{2}+5=9=>P\left(-1;3\right)kothuocHS\)
\(f\left(\frac{1}{2}\right)=\frac{1}{2}.\frac{1}{4}-\frac{7}{2}.\frac{1}{2}+5=\frac{\left(1-14+5.8\right)}{8}=\frac{27}{8}=>Qkothuoc\)
c)
\(\frac{1}{2}x^2-\frac{7}{2}x+5=-3\Rightarrow\frac{1}{2}x^2-\frac{7}{2}x+8=0\)
\(x^2-7x+16=0\Leftrightarrow\left(x^2-2.\frac{7}{2}x+\frac{49}{4}\right)+\frac{15}{4}\)vo nghiem

Do điểm M(a; -0,2) thuộc đồ thị của hàm số y = 4x nên thay x = a và y = -0,2 vào ta được:
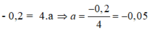
Đáp số : (C).

a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
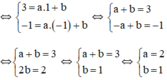
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.

a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
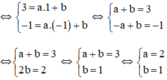
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đồ thị hàm số y = 0,2 x 2 đi qua điểm C(c; 6) nên tọa độ điểm C nghiệm đúng phương trình hàm số.
Ta có : 6 = 0,2. c 2 ⇔ c 2 = 6/(0,2) = 30 ⇒ c = ± 30
Điểm D(c; -6) đối xứng với điểm C(c; 6) qua trục hoành mà đồ thị hàm số y = 0,2 x 2 gồm hai nhánh đối xứng qua trục tung nên điểm C(c ; 6) thuộc đồ thị hàm số thì điểm D(c ; -6) không thuộc đồ thị hàm số.