Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a. Biết SA = a và vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (SCD) bằng φ , với cos φ = 2 5 . Tính theo a thể tích của khối chóp S.ABCD
A. 4 3 a 3
B. 2 3 a 3
C. 2 a 3
D. a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

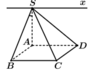
• Giao tuyến của (SBC) và (SAD) là
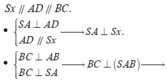
![]()
![]() (do tam giác SAB vuông cân).
(do tam giác SAB vuông cân).
Chọn B.

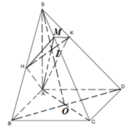
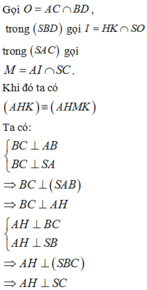
Hoàn toàn tương tự ta chứng minh được
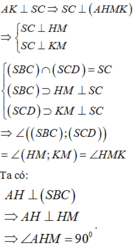
Tương tự ta có
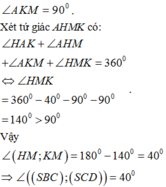
Chọn A.

a) Ta có:
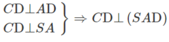
⇒ (SCD) ⊥ (SAD)
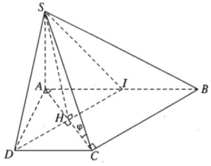
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
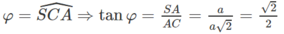
c) 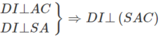
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 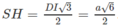 .
.
Tam giác SDI có diện tích:
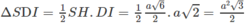
Chọn B.
+ Gọi AD = x (x > 0)
+ Kẻ dễ dàng chứng minh được
dễ dàng chứng minh được 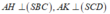
Trong tam giác SBC ta có
Trong tam giác SAD có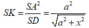
Xét tam giác AHK có
Xét tam giác AHK có
Vậy