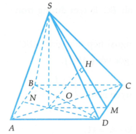
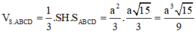Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD,d(G,(SAD))=a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC.
A. 2a
B. 3a
C. 4a
D. 3 2 a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 1 2019
Đúng(0)
Những câu hỏi liên quan
CM
9 tháng 5 2018
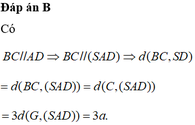
Chọn đáp án A.
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên S D G ^ nhọn
CM
4 tháng 1 2020
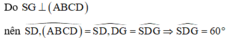
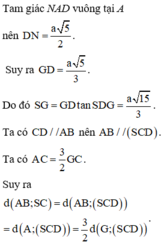
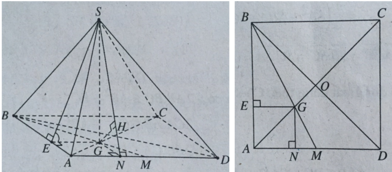
+ Xác định góc của (SAB) và mặt phẳng đáy.
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:
AB ⊥ SG & AB ⊥ GE⇒ AB ⊥ (SEG) ⇒ AB ⊥ SE.
SE ⊥ AB & GE ⊥ AB⇒ ∠((SAB),(ABCD)) = ∠(SEG) = 60o.
+ Xác định khoảng cách từ B đến mặt phẳng (SAD).
Hạ GN ⊥ AD. Tương tự như trên, ta có: AD ⊥ GN & AD ⊥ SG⇒ AD ⊥ (SGN)
Hạ GH ⊥ SN, ta có GH ⊥ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.
+ Tính GH.
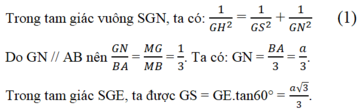
(do GE = GN). Thế vào (1) ta được:
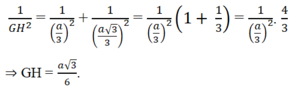
Ta có: M ∈(SAD) & MB = 3MG⇒ d(B,(SAD)) = 3d(G,(SAD)) = (a√3)/2.
CM
2 tháng 4 2019
Đáp án C
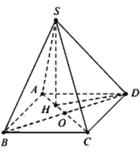
Phương pháp giải:
Xác định hình chiếu của đỉnh, xác định góc để tìm chiều cao và áp dụng công thức thể tích
Lời giải:
Gọi O là tâm hình vuông ABCD , H là trọng tâm tam giác ABD
Ta có 
ABCD là hình vuông cạnh a nên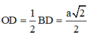 
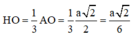
Tam giác HDO vuông tại O, có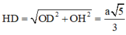 
Tam giác SHD vuông tại H, có 
Vậy thể tích cần tính là 
