
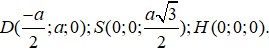

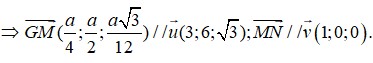

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

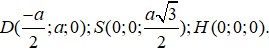

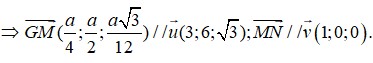


Chọn đáp án C
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên S O ⊥ A B C D
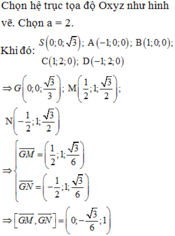
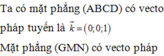

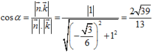

Đáp án B
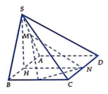
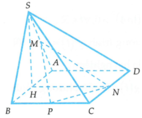
Gọi H là trung điểm của cạnh AB. Khi đó S H ⊥ ( A B C D )
Ta có S H ⊥ A B ; A B ⊥ H N ; H N ⊥ S H và S H = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:
B ( 1 ; 0 ; 0 ) ; A ( - 1 ; 0 ; 0 ) ; N ( 0 ; 2 3 ; 0 ) ; C ( 1 ; 2 3 ; 0 ) ; D ( - 1 ; 2 3 ; 0 ) ; S ( 0 ; 0 ; 3 ) ; M ( - 1 2 ; 0 ; 3 2 ) ; P ( 1 ; 3 ; 0 )
Mặt phẳng (SCD) nhận n 1 → = - 3 6 C D → , S C → = 0 ; 1 ; 2 làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận n 2 → = - 2 3 3 M N → , M P → = 3 ; 1 ; 5 làm một vectơ pháp tuyến.
Gọi ∅ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
cos ∅ = n 1 → . n 2 → n 1 → . n 2 → = 11 145 145

Chọn đáp án B.

Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:


Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án C.
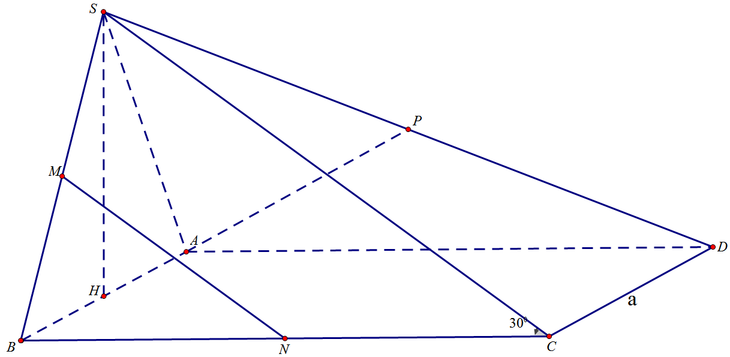
Trong không gian Oxyz:
Chọn A ≡ O 0 ; 0 ; 0 ; B a ; 0 ; 0 ; D 0 ; a ; 0 ; C a ; a ; 0
⇒ H a 2 ; 0 ; 0 ; S a 2 ; 0 ; a 3 2 ; M 3 a 4 ; 0 ; a 3 4 ; N a ; a 2 ; 0 ; P a 4 ; a 2 ; a 3 4
Ta có:
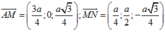
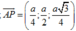

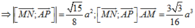
⇒ d M N ; A P = M N → ; A P → . A M → M N → ; A P → = 3 5 10 a