Cho hàm số f x = a x 3 + b x 2 + c x + d với a , b , c , d là các hệ số thực và a ≠ 0 . Hàm số f x nghịch biến trên ℝ khi và chỉ khi:
A. a < 0 b 2 ≤ 3 a c
B. a < 0 b 2 < 3 a c
C. a > 0 b 2 ≥ 3 a c
D. a > 0 b 2 < 3 a c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
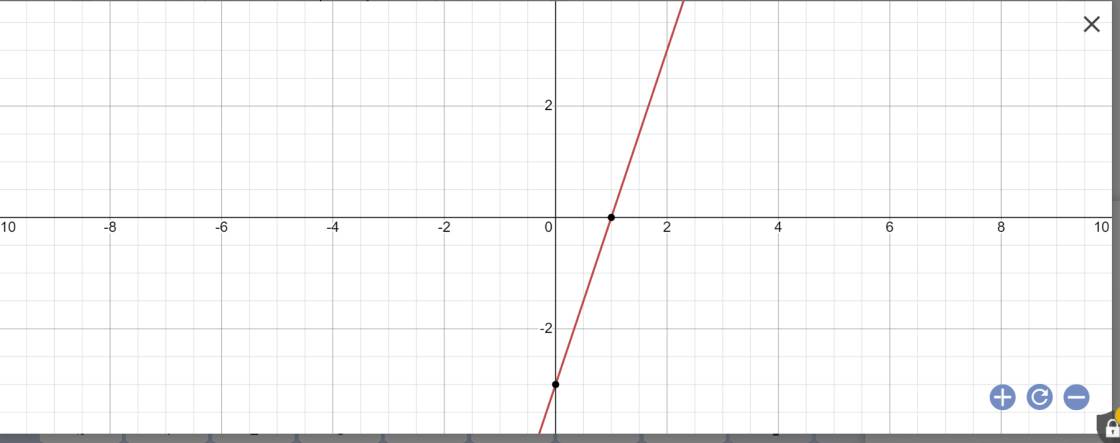
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2

Đáp án D
Ta có hàm số g x = f x - 2018 là hàm số bậc ba liên tục trên R.
Do a>0 nên l i m x → - ∞ g ( x ) = - ∞ ; l i m x → + ∞ g ( x ) = + ∞
Để ý g 0 = d - 2018 > 0 ; g 1 = a + b + c + d - 2018 < 0 nên phương trình g(x)=0 có đúng 3 nghiệm phân biệt trên R.
Khi đó đồ thị hàm số g x = f x - 2018 cắt trục hoành tại 3điểm phân biệt nên hàm số y = f x - 2018 có đúng 5 cực trị.
Chọn A
Ta có: f ' x = 3 a x 2 + 2 b x + c
có ∆ ' f ' x = b 2 - 3 a c .
Hàm số f x nghịch biến trên ℝ khi và chỉ khi
3 a < 0 ∆ ' f ' x ≤ 0