Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần I
Câu 1: c,d
Câu 2: e
Phần II
Câu 1:
a, 2008a2-2008b2=2008(a2-b2)=2008(a-b)(a+b)
b, x2-8x+15=x2-3x-5x-+15=x(x-3)-5(x-3)=(x-5)(x-3)
Câu 2:
a, M= (x-3)(x+3)-(x+2)2-2(x2-4,5)
M= x2-9-(x2+4x+4)-2x2+9
M= x2-9-x2-4x-4-2x2+9
M= -2x2-4x-4
M= -2(x2+2x+2)b, Để M=0 -> -2(x2+2x+2)=0->x2+2x+2=0
Phần 1:
Câu 1: D
Câu 2: E
Phần 2:
Câu 1:
\(A=2008a^2-2008b^2\)
\(=2008\left(a^2-b^2\right)\)
\(=2008\left(a-b\right)\left(a+b\right)\)
\(B=x^2-8x+15\)
\(=x^2-3x-5x+15\)
\(=x\left(x-3\right)-5\left(x-3\right)\)
\(=\left(x-3\right)\left(x-5\right)\)
Câu 2:
\(M=\left(x-3\right)\left(x+3\right)-\left(x+2\right)^2-2\left(x^2-4,5\right)\)
\(=x^2-9-x^2-4x-4-2x^2+9\)
\(=-2x^2-4x-4\)
\(=-2\left(x^2+2x+2\right)\)
\(=-2\left[\left(x^2+2x+1\right)+1\right]\)
\(=-2\left[\left(x+1\right)^2+1\right]\)
\(=-2-2\left(x+1\right)^2\le-2< 0\)
Vậy không có giá trị nào của x thoả mãn yêu cầu.

BÀI 1:
a) \(ĐKXĐ:\) \(\hept{\begin{cases}x-2\ne0\\x+2\ne0\end{cases}}\) \(\Leftrightarrow\)\(\hept{\begin{cases}x\ne2\\x\ne-2\end{cases}}\)
b) \(A=\left(\frac{2}{x-2}-\frac{2}{x+2}\right).\frac{x^2+4x+4}{8}\)
\(=\left(\frac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right).\frac{\left(x+2\right)^2}{8}\)
\(=\frac{2x+4-2x+4}{\left(x-2\right)\left(x+2\right)}.\frac{\left(x+2\right)^2}{8}\)
\(=\frac{x+2}{x-2}\)
c) \(A=0\) \(\Rightarrow\)\(\frac{x+2}{x-2}=0\)
\(\Leftrightarrow\) \(x+2=0\)
\(\Leftrightarrow\)\(x=-2\) (loại vì ko thỏa mãn ĐKXĐ)
Vậy ko tìm đc x để A = 0
p/s: bn đăng từng bài ra đc ko, mk lm cho

1: \(\dfrac{A}{B}=\dfrac{4}{3}x^{n+1-3}y^{2-n+1}=\dfrac{4}{3}x^{n-2}y^{3-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-2>=0\\3-n< =0\end{matrix}\right.\Leftrightarrow2< =n< =3\)
2: \(\dfrac{A}{B}=\dfrac{7}{5}x^{n-1-2}y^{5-n}-xy^{4-n}=\dfrac{7}{5}x^{n-3}y^{5-n}-xy^{4-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-3>=0\\5-n>=0\\4-n>=0\end{matrix}\right.\Leftrightarrow3\le n\le4\)

Answer:
Câu 1:
\(\left(5x-x-\frac{1}{2}\right)2x\)
\(=\left(4x-\frac{1}{2}\right)2x\)
\(=4x.2x-\frac{1}{2}.2x\)
\(=8x^2-x\)
\(\left(x^3+4x^2+3x+12\right)\left(x+4\right)\)
\(=x\left(x^3+4x^2+3x+12\right)+4\left(x^3+4x^2+3x+12\right)\)
\(=x^4+4x^3+3x^2+12x+4x^3+16x^2+12x+48\)
\(=x^4+\left(4x^3+4x^3\right)+\left(3x^2+16x^2\right)+\left(12x+12x\right)+48\)
\(=x^4+8x^3+19x^2+24x+48\)
Ta thay \(x=99\) vào phân thức \(\frac{x^2+1}{x-1}\): \(\frac{\left(99\right)^2+1}{99-1}=\frac{9802}{98}=\frac{4901}{49}\)
Ta thay \(x=4\) vào phân thức \(\frac{x^2-x}{2\left(x-1\right)}\) : \(\frac{4^2-4}{2.\left(4-1\right)}=\frac{12}{6}=2\)
\(\left(x+y\right)^2-\left(x-y\right)^2\)
\(= (x²+2xy+y²)-(x²-2xy+y²)\)
\(= x²+2xy+y²-x²+2xy-y²\)
\(= 4xy\)
\(4x^2+4x+1=\left(2x+1\right)^2=\left(2.2+1\right)^2=25\)
Câu 2:
\(x^2+x=0\)
\(\Rightarrow x\left(x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
\(x^2.\left(x-1\right)+4-4x=0\)
\(\Rightarrow x^2.\left(x-1\right)+4\left(1-x\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x^2-4\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)=0\)
Trường hợp 1: \(x-1=0\Rightarrow x=1\)
Trường hợp 2: \(x-2=0\Rightarrow x=2\)
Trường hợp 3: \(x+2=0\Rightarrow x=-2\)
Câu 3: Bạn xem lại đề bài nhé.

Bài 1: Giả sử \(C\ge0\)
Ta có:
\(C=b^3-a^3-6b^2-a^2+9b\ge0\)
\(\Leftrightarrow\left(b^3-6b^2+9b\right)-\left(a^3+a^2\right)\ge0\Leftrightarrow b\left(b^2-6b+9\right)-a^2\left(a+1\right)\ge0\)
\(\Leftrightarrow b\left(b-3\right)^2-a^2\left(a+1\right)\ge0\)
Mà \(a+b=3\Rightarrow b=3-a\)
\(\Rightarrow C=\left(3-a\right)\left(3-a-3\right)^2-a^2\left(a+1\right)\ge0\Leftrightarrow a^2\left(3-a\right)-a^2\left(a+1\right)=a^2\left(2-2a\right)\ge0\)
Ta có: \(a^2\ge0;a\le0\Rightarrow2a\le0\Rightarrow-2a\ge0\Rightarrow2-2a\ge2\Rightarrow C\ge0\)(luôn đúng)
Bài 2: để suy nghĩ đã á

1. cho các số thực dương x,y,z t/mãn: x2 + y2 + z2 = 1
Cmr: \(\frac{x}{y^2+z^2}\) + \(\frac{y}{x^2+z^2}+\frac{z}{x^2+y^2}\ge\) \(\frac{3\sqrt{3}}{2}\)
2. Cho x,y thỏa mãn \(\hept{\begin{cases}xy\ge0\\x^2+y^2=1\end{cases}}\)
Tìm GTNN,GTLN của \(S=x\sqrt{1+y}+y\sqrt{1+x}\)
3. Cho \(\hept{\begin{cases}xy\ne0\\xy\left(x+y\right)=x^2+y^2-xy\end{cases}}\)
Tìm GTLN của \(A=\frac{1}{x^3}+\frac{1}{y^3}\)
4. Cho tam giác ABC; đường thẳng đi qua trọng tâm G và tâm đường tròn nội tiếp I vuông góc với đường phân giác trong của góc C. Gọi a,b,c là độ dài 3 canh tương ứng với 3 đỉnh A,B,C.
Cmr: \(\frac{1}{a}+\frac{1}{b}\le\frac{2}{c}\)
ui má. đúng mấy bài tập thầy tui cho ôn. giờ đang loay hoay
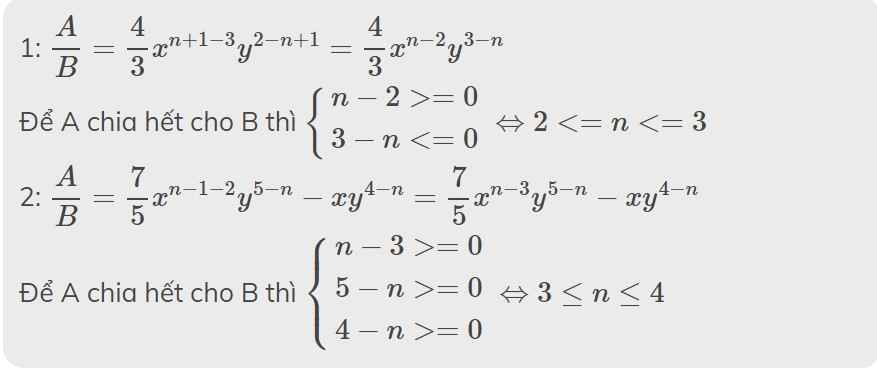
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2