Cho tứ diện ABCD có (ACD) ⊥ (BCD), AC = AD = BC = BD = a, CD = 2x . Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:
A. a 2 3
B. a 3 3
C. a 3 2
D. a 5 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Xác định góc giữa hai mặt phẳng (ABC); (ABD), tìm điều kiện của x để góc đó bằng 900
Cách giải:
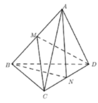
Gọi M là trung điểm của AB ta có :
Tam giác ABC cân tại C => CM ⊥ AB
Tam giác ABD cân tại D => DM ⊥ AB
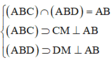
![]()
Để ![]()
![]() vuông tại M
vuông tại M
Gọi N là trung điểm của CD, chứng minh tương tự như trên ta có:
![]()
Xét tam giác vuông ANC có:
![]()
![]()
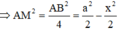
Xét tam giác vuông ACM có: 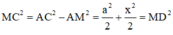
Để ∆CDM vuông tại M ![]()
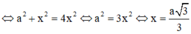

Chọn C
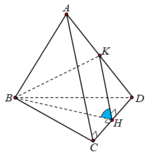
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
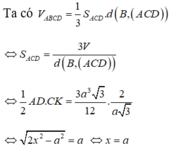
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
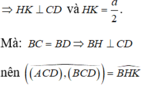
Mặt khác:
Tam giác ABD có:
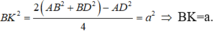
Tam giác BHK có:
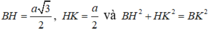
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o

Đáp án D
![]()
nên ∆ BCDlà tam giác đều.
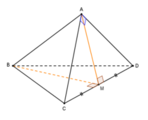
![]()
nên theo định lý Py-ta-go đảo, ta có ∆ ACD vuông cân tại A .
Khi đó, gọi M là trung điểm CD thì: AM ⊥ CD và BM ⊥ CD Ta có:
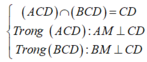
![]()
∆
BCD đều có đường cao
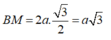
∆
ACD vuông cân tại A nên trung tuyến
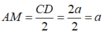
Áp dụng định lý hàm cos trong
∆
AMB, ta có:
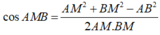
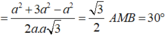
![]()
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) có số đo bằng 30 o

Đáp án C
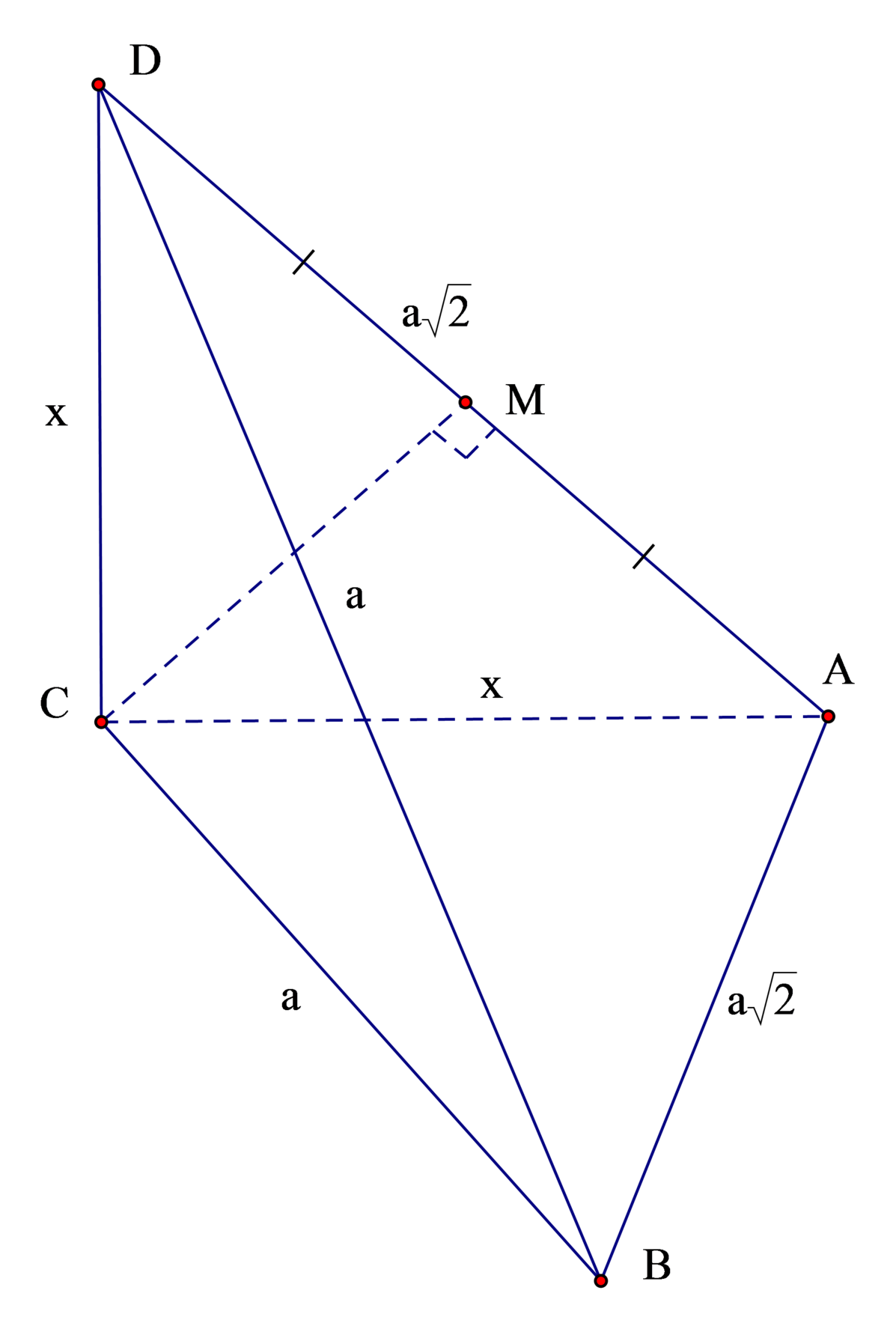
Gọi h là khoảng cách từ B → A C D
⇒ h = a 3 2 ⇒ S Δ A C D = 3 V A B C D h = 3 a 3 3 12 a 3 2 = a 2 2
Gọi M là trung điểm AD ⇒ C M ⊥ A D .
⇒ C M = 2 S A C D A D = 2. a 2 2 a 2 = a 2 2 = 1 2 A D
⇒ Δ A C D vuông tại C ⇒ C A = C D = a
Δ C A D = Δ C B A C . C . C ⇒ A C D ^ = A C B ^ = 90 0
⇒ A C ⊥ C D A C ⊥ C B ⇒ A C ⊥ B C D ⇒ A C D ⊥ B C D
Hay góc giữa hai mặt phẳng bằng 90 0
Phương pháp:
Xác định góc giữa hai mặt phẳng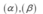
- Tìm giao tuyến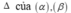
- Xác định 1 mặt phẳng
- Tìm các giao tuyến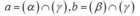
- Góc giữa hai mặt phẳng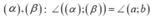
Cách giải:
Gọi M là trung điểm của CD.
Do tam giác ACD và BCD là các tam giác cân tại A, B
và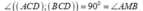
Dễ dàng chứng minh được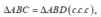
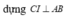 tại I
tại I
suy ra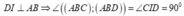
Lại có: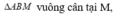
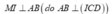
Từ (1), (2) suy ra: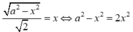
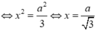
Chọn: B