


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Chọn A
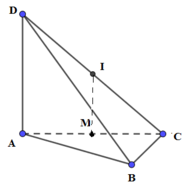
Coi như a = 1 . Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ B C D và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ A H E ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 πa 3

Gọi H là trung điểm BC
Vì \(\Delta BDC\) vuông tại D nên H là tâm đường tròn ngoại tiếp \(\Delta BDC\)
Vì \(\Delta ABC\) cân tại A nên AH vuông góc với BC
Mà (ABC) vuông góc (BDC) nên AH vuông góc với (BDC) tại H
\(\Rightarrow\) tâm mặt cầu ngoại tiếp tứ diện ABCD phải nằm trên đường thẳng AH
Chọn điểm O thuộc đường thẳng AH sao cho OA=OB thì O chính là tâm mặt cầu cần tìm
(bạn tự tính) được \(R=\frac{a^2}{b}\)

Đáp án D
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:
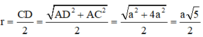

Chọn C
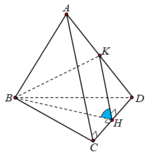
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
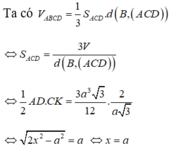
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
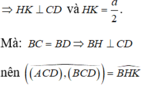
Mặt khác:
Tam giác ABD có:
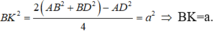
Tam giác BHK có:
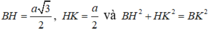
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o

Phương pháp:
Xác định góc giữa hai mặt phẳng ![]()
- Tìm giao tuyến ![]()
- Xác định 1 mặt phẳng ![]()
- Tìm các giao tuyến ![]()
- Góc giữa hai mặt phẳng ![]()
Cách giải:
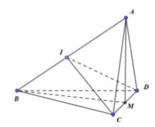
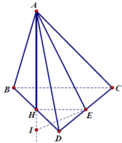
Gọi M là trung điểm của CD.
Do tam giác ACD và BCD là các tam giác cân tại A, B
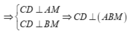
và ![]()
Dễ dàng chứng minh được ![]()
![]() tại I
tại I
suy ra ![]()
![]()
![]()
Lại có: ![]()
![]()
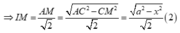
Từ (1), (2) suy ra: 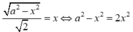
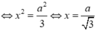
Chọn: B