Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 1 = y 1 = z + 2 1 và điểm M(2;-1;0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn ?
A. 2.
B. 1.
C. 0.
D. Vô số.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

Chọn A
Vì A thuộc ![]() nên A (1+2t;1-t;-1+t).
nên A (1+2t;1-t;-1+t).
Vì B thuộc ![]() nên B (-2+3t';-1+t';2+2t').
nên B (-2+3t';-1+t';2+2t').

Thay vào (3) ta được t=1, t'=2 thỏa mãn.

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương u → 2 ; - 1 ; 3 .

Đáp án B
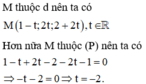
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Chọn A

Gọi I = d ∩ Δ. Do I ∈ Δ nên I (2t + 1; t – 1; -t).

từ đó suy ra d có một vectơ chỉ phương là ![]() và đi qua M (2 ; 1 ; 0) nên có phương trình
và đi qua M (2 ; 1 ; 0) nên có phương trình 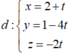
Đáp án B.
Phương pháp giải: Gọi tọa độ điểm, tính khoảng cách và tìm tọa độ tâm thông qua bán kính
Lời giải: Ta có
Phương trình mặt phẳng (Oxy): z=0
Khoảng cách từ tâm I đến mp(Oxy) là
Theo bài ra, ta có