Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số g(x) = f( 4 x - x 2 ) + 1 3 x 3 - 3 x 2 + 8 x + 1 3 trên đoạn [1;3].
A. 15
B. 25 3
C. 19 3
D. 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có g ( x ) = f ( 2 x ) - sin 2 x ≤ f ( 2 x ) 2 x ∈ - 2 ; 2 suy ra bảng biến thiên
Dựa vào BBT suy ra f ( 2 x ) ≤ f ( 0 ) ⇒ g ( x ) ≤ f ( 0 ) ∀ 2 x ∈ - 2 ; 2
⇒ m a x [ - 1 ; 1 ] g ( x ) = f ( 0 ) đạt được khi
x = 0 sin 2 x = 0 ⇔ x = 0
Chọn đáp án B.

g ' ( x ) = f ' ( x ) - 1 ; g ' ( x ) = 0 ⇔ f ' ( x ) = 1
Dựa vào bảng biến thiên của hàm số y = f ' ( x ) ta có
f ' ( x ) = 1 ⇔ [ x = - 1 x = x 0 > 1
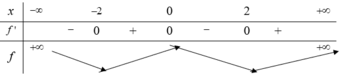
Bảng xét dấu g ' ( x )

Vậy hàm số g(x)=f(x)-x có một điểm cực trị.
Chọn đáp án D.

Chọn C
Xét hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2]
![]()
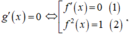
Từ bảng biến thiên, ta có:
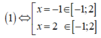
Và ![]() nên f(x) đồng biến trên [-1;2]
nên f(x) đồng biến trên [-1;2]
![]()
![]() nên (2) vô nghiệm
nên (2) vô nghiệm
Do đó, g'(x) = 0 chỉ có nghiệm là x = -1 và x = 2
Ta có ![]()
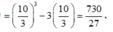
![]()
Vậy ![]()

Chọn B
Đặt ![]()
Bài toán quy về tìm giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0].
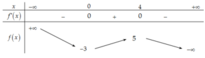
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0] là 3.
Vậy giá trị lớn nhất của hàm số f(sin x -1) bằng 3.
Chọn D
Với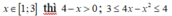
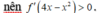
Suy ra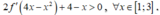
Bảng biến thiên
Suy ra