Question

[Vũ Đình Chung]

Cho điểm C thuộc nửa đường tròn (O;R) đường kính MN với C khác M, C khác N và CM < CN. Trên nửa mặt phẳng bờ MN chứa điểm C, kẻ các tia tiếp tuyến Mx, Ny với (O). Tiếp tuyến tại C của (O) cắt Mx, Ny lần lượt tại A, B.
1. Chứng minh tứ giác ACOM nội tiếp.
2. Cho OB = 2R. Tính độ dài đoạn BN theo R và số đo NBC.
3. Gọi I là giao điểm của AN với BM, E giao điểm của OA với CM và F là giao điểm của OB với CN. Chứng minh CI vuông góc MN và ba điểm E, I, F thẳng hàng.

Answer 1

[Nguyễn Ngọc Anh Minh]

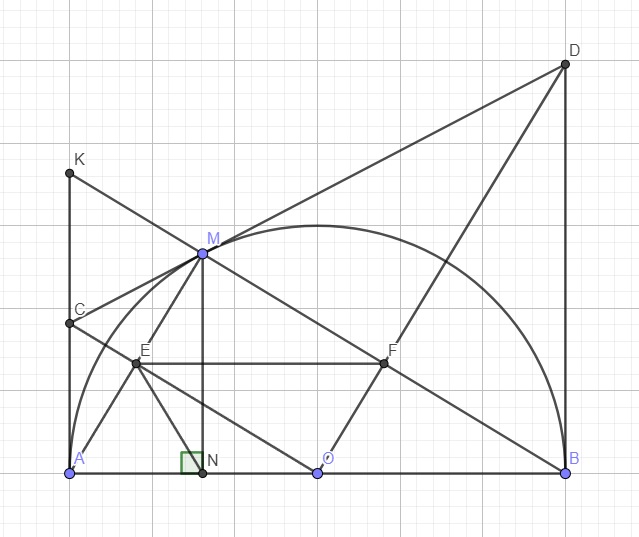
a/ C và M cùng nhìn AO dưới 1 góc vuông => C và M thuộc đường tròn đường kính AO => ACOM là tư giác nội tiếp

b/

Xét tg vuông BON có

\(BN=\sqrt{OB^2-ON^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)

\(\sin\widehat{OBN}=\frac{ON}{OB}=\frac{R}{2R}=\frac{1}{2}\Rightarrow\widehat{OBN}=30^o\)

Ta có \(BN=BC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm băng nhau)

Xét tg vuông BOC

\(\sin\widehat{OBC}=\frac{OC}{OB}=\frac{R}{2R}=\frac{1}{2}\Rightarrow\widehat{OBC}=30^o\)

\(\Rightarrow\widehat{NBC}=\widehat{OBN}+\widehat{OBC}=30^o+30^o=60^o\)

c/

Ta có 

E; F là trung điểm của CM và CN (hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm vuông góc và chia đôi dây cung nối 2 tiếp điểm)

=> EF là đường trung bình của \(\Delta MCN\) => EF//MN (1)

Ta có

\(AM\perp MN;BN\perp MN\) => AM//BN \(\Rightarrow\frac{IA}{IN}=\frac{IM}{IB}=\frac{AM}{BN}\) (talet trong tam giác)

Mà \(AM=AC;BN=BC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm băng nhau)

\(\Rightarrow\frac{IA}{IN}=\frac{IM}{IB}=\frac{AC}{BC}\) (2)

Ta có

\(\widehat{MCN}=90^o\) (góc nội tiếp chắn nửa đường tròn)

\(CM\perp AO;CN\perp BO\left(cmt\right)\Rightarrow\widehat{MCN}=\widehat{AOB}=90^o\)

\(\Rightarrow CM\perp AO;BO\perp AO\) => CM//BO

Xét \(\Delta ABO\) có CM//BO \(\Rightarrow\frac{EA}{EO}=\frac{AC}{BC}\) (3)

Từ (2) và (3) \(\Rightarrow\frac{EA}{EO}=\frac{IA}{IN}\)

Nối E với I, xét \(\Delta AON\) có \(\frac{EA}{EO}=\frac{IA}{IN}\) => EI//MN (Talet đảo trong tam giác) (4)

Từ (1) và (4) => EF trung EI (Từ 1 điểm ngoài 1 đường thẳng chỉ duy nhất dựng được 1 đường thẳng // với đường thẳng đã cho)

=> E; I; F thẳng hàng