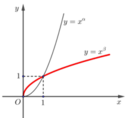
Cho các số thực
α
và
β
. Đồ thị các hàm số
y
=
x
β
,
y
=
x
β
trên khoảng
0
;
+
∞
như hình vẽ bên, trong đó đường đậm hơn là đồ thị của hàm số
y
=
x
β
.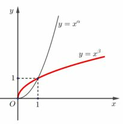
Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()