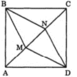
Trong hình vuông ABCD ta chia đoạn thẳng AC thành 3 đoạn thẳng AM, MN, NC bằng nhau. So sánh diện tích các hình tam giác ABM, MBN, NBC, MDA, NCD và MDN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2023
a: Xét ΔOBA và ΔODC có
góc OBA=góc ODC
góc BOA=góc DOC
=>ΔOBA đồng dạng với ΔODC
=>OB/OD=OA/OC=AB/CD=1/3
=>S ABO=1/3*S ABC
=>S BOC=2/3*S ABC
b: Kẻ CH vuông góc AB
=>S ABC=1/2*CH*AB
S ABCD=1/2*CH*(AB+CD)
=>S ABC/S ABCD=AB/(AB+CD)
Diện tích tam giác ABC = 3 x diện tích ABM = 3 x diện tích MBN = 3 x diện tích NBC (vì có chung đường cao vẽ từ B đến AC và AM = MN = NC = 1/3 x AC)
Diện tích tam giác ADC = 3 x diện tích MDA = 3 x diện tích MND = 3 x diện tích NCD (vì có chung đường cao vẽ từ D đến AC; AM = MN = NC = 1/3 AC)
Mặt khác diện tích tam giác ABC bằng diện tích tam giác ADC (ABCD là hình vuông)