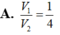
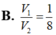
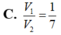
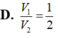
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Ta có: V 1 V = 1 3 π . S I ' . I ' M 2 1 3 π . S I . I A 2 = = 1 8 ⇒ V 1 V 2 = 1 7 .
Đáp án D.
Gọi h,r là chiều cao và bán kính đáy của khối nón lớn.
Theo đó, chiều cao và bán kính của khối nón nhỏ lần lượt là h 2 và r 2
Tỉ số thể tích khối nón nhỏ và khối nón lớn là: π 3 r 2 2 h 2 πr 2 h 3 = 1 8
Vậy tỉ số thêt tích của 2 phần được chia là: 1 7 .
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow\widehat{SMO}=60^0\)
\(\Rightarrow SO=OM.tan60^0=\dfrac{a\sqrt{3}}{2}\)
Trong mp (ABCD), kéo dài AM và CD cắt nhau tại E
Trong mp (SCD), nối NE cắt SC tại F
Theo định lý talet: \(\dfrac{EC}{ED}=\dfrac{MC}{AD}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}EC=a\\ED=2a\end{matrix}\right.\)
Áp dụng định lý Menelaus cho tam giác SCD:
\(\dfrac{FS}{FC}.\dfrac{CE}{ED}.\dfrac{DN}{NS}=1\Leftrightarrow\dfrac{FS}{FC}.\dfrac{1}{2}.1=1\Rightarrow\dfrac{FS}{FC}=2\)
\(\Rightarrow\dfrac{FC}{SC}=\dfrac{1}{3}\Rightarrow d\left(F;\left(ABCD\right)\right)=\dfrac{1}{3}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{3}SO=\dfrac{a\sqrt{3}}{6}\)
\(ND=\dfrac{1}{2}SD\Rightarrow d\left(N;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{2}SO=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow V_{NADMFC}=V_{NADE}-V_{FMCE}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{4}.\dfrac{1}{2}a.2a-\dfrac{1}{3}.\dfrac{a\sqrt{3}}{6}.\dfrac{1}{2}.a.\dfrac{a}{2}=\dfrac{5\sqrt{3}}{72}a^2\)
\(\Rightarrow V_1=V_{SABCD}-V_{NADMFC}=....\)
