Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau? 3 x 2 + 2 5 x - 3 3 và - x 2 - 2 3 x +2 5 +1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2018
Ta có: x 2 - 2 3 x - 3 = 2 x 2 +2x + 3
⇔ x 2 - 2 3 x - 3 - 2 x 2 -2x - 3 =0
⇔ x 2 +2x +2 3 x +2 3 =0
⇔ x 2 + 2(1 + 3 )x + 2 3 =0
∆ ' = b ' 2 – ac= 1 + 3 2 – 1. 2 3 = 1 + 2 3 + 3 -2 3 = 4 > 0
∆ ' = 4 =2
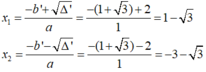
Vậy với x=1 - 3 hoặc x = - 3 - 3 thì giá trị của hai biểu thức trên bằng nhau
PT
1
CM
11 tháng 10 2019
Ta có: 3 x 2 + 2x -1 = 2 3 x + 3 ⇔ 3 x 2 + 2x - 2 3 x -3 -1 = 0
⇔ 3 x 2 + (2 - 2 3 )x -4 =0 ⇔ 3 x 2 + 2(1 - 3 )x -4 = 0
∆ ' = b ' 2 – ac= 1 - 3 2 - 3 (-4) =1 - 2 3 +3 +4 3
= 1 + 2 3 +3 = 1 - 3 2 > 0
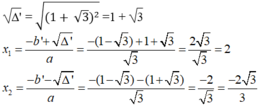
Vậy với x= 2 hoặc x = (-2 3 )/3 thì giá trị của hai biểu thức trên bằng nhau
PT
Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau? -2 2 x – 1 và 2 x 2 + 2x +3
1
CM
17 tháng 12 2017
Ta có: -2 2 x – 1 = 2 x 2 + 2x +3 ⇔ 2 x 2 +2x + 3 + 2 2 x + 1=0
⇔ 2 x 2 + 2(1 + 2 )x +4 =0
∆ ' = b ' 2 – ac= 1 + 2 2 - √2 .4= 1+2 2 +2 - 4 2
= 1-2 2 +2 = 2 - 1 2 > 0
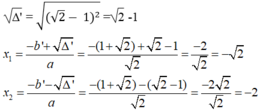
Vậy với x= - 2 hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau
PT
1
CM
16 tháng 2 2019
Ta có: x 2 +2 + 2 2 = 2(1 + 2 )x ⇔ x 2 - 2(1+ 2 )x +2 +2 2 = 0
∆ ' = b ' 2 – ac = - 1 + 2 2 - 1(2+2 2 )
= 1 + 2 2 +2 -2 -2 2 =1 > 0
∆ ' = 1 =1
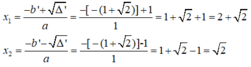
Vậy với x= 2+ 2 hoặc x = 2 thì giá trị của hai biểu thức trên bằng nhau
CM
9 tháng 3 2018
Từ giả thiết suy ra (x + 1)2 - 4 ≤ (x - 3)2
Û x2 + 2x + 1 - 4 ≤ x2 - 6x + 9
Û x2 + 2x + 1 - 4 - x2 + 6x - 9 ≤ 0
Û 8x ≤ 12
Û x ≤ 3/2
Vậy x ≤ 3/2là giá trị cần tìm.
Đáp án cần chọn là: C
TD
1
12 tháng 3 2020
Bài 2:
(1 + x)3 + (1 - x)3 - 6x(x + 1) = 6
<=> x3 + 3x2 + 3x + 1 - x3 + 3x2 - 3x + 1 - 6x2 - 6x = 6
<=> -6x + 2 = 6
<=> -6x = 6 - 2
<=> -6x = 4
<=> x = -4/6 = -2/3
Bài 3:
a) (7x - 2x)(2x - 1)(x + 3) = 0
<=> 10x3 + 25x2 - 15x = 0
<=> 5x(2x - 1)(x + 3) = 0
<=> 5x = 0 hoặc 2x - 1 = 0 hoặc x + 3 = 0
<=> x = 0 hoặc x = 1/2 hoặc x = -3
b) (4x - 1)(x - 3) - (x - 3)(5x + 2) = 0
<=> 4x2 - 13x + 3 - 5x2 + 13x + 6 = 0
<=> -x2 + 9 = 0
<=> -x2 = -9
<=> x2 = 9
<=> x = +-3
c) (x + 4)(5x + 9) - x2 + 16 = 0
<=> 5x2 + 9x + 20x + 36 - x2 + 16 = 0
<=> 4x2 + 29x + 52 = 0
<=> 4x2 + 13x + 16x + 52 = 0
<=> 4x(x + 4) + 13(x + 4) = 0
<=> (4x + 13)(x + 4) = 0
<=> 4x + 13 = 0 hoặc x + 4 = 0
<=> x = -13/4 hoặc x = -4
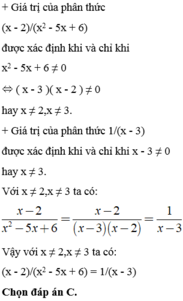
Ta có: 3 x 2 + 2 5 x - 3 3 = - x 2 - 2 3 x +2 5 +1
⇔ 3 x 2 + 2 5 x - 3 3 + x 2 + 2 3 x - 2 5 – 1= 0
⇔ ( 3 +1) x 2 + (2 5 + 2 3 )x -3 3 - 2 5 – 1= 0
⇔ ( 3 +1)x2 + 2( 5 + 3 )x -3 3 - 2 5 – 1= 0
∆ ' = b ' 2 – ac= 3 + 5 2 – ( 3 + 1 )( -3 3 - 2 5 – 1)
= 5 + 2 15 +3+9 +2 15 + 3 +3 3 +2 5 + 1
=18 +4 15 +4 3 +2 5
= 1 + 12 + 5 + 2.2 3 + 2 5 + 2.2 3 . 5
= 1 + 2 3 2 + 5 2 + 2.1.2 3 +2.1. 5 + 2.2 5 . 3
= 1 + 2 3 + 5 2 > 0