Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AB = a, BC = a, CD = a 6 , SA = a 6 . Khi SA ⊥ (ABCD) thì khoảng cách từ giữa AD và SC là?

A. a 5 3
B. a 5 2
C. a 6 3
D. a 6 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
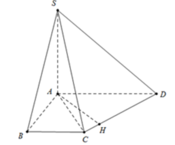
Dựng A H ⊥ C D suy ra AH là đường vuông góc cung của SA vad CD Ta có:
S A C D = 1 2 A D . d C ; A D = 1 2 .3 a . A B = 3 a 2 2 .
Lại có:
C D = A B 2 + A D − B C 2 = a 5 ⇒ A H = 2 S A C D C D = 3 a 5

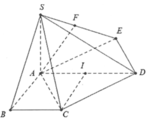
HD: Gọi I là trung điểm của AD → ABCI là hình vuông cạnh a → ∆ACI có đường trung tuyến
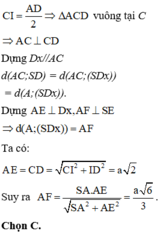

Chọn B.
Phương pháp:
Gắn hệ trục tọa độ.
Cách giải:

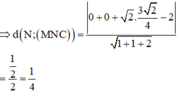
Vây, khoảng cách từ N đến mặt phẳng (MCD) bằng: 1 4 a

Cách 1:

Gọi I là trung điểm của cạnh AD.
∆ A B C vuông cân tại B, ∆ I C D vuông cân tại I và có AB=IC=a nên A C = C D = a 2
Khi đó A C 2 + C D 2 = A D 2 nên ∆ A C D vuông cân tại C.
Trong (ABCD), dựng hình vuông ACDE. Trong ∆ S A E , kẻ A H ⊥ S E ( 1 )
Ta có
E D ⊥ S A E D ⊥ A E ⇒ E D ⊥ ( S A E ) ⇒ E D ⊥ A H ( 2 )
Từ (1) và (2) suy ra A H ⊥ ( S D E )
Vì A C / / E D nên
d A C , S D = d A C , S D E = d A ; S D E = A H
Trong ∆ S A E , 1 A H 2 = 1 S A 2 + 1 A E 2
⇔ A H = S A . A E S A 2 = A E 2 ⇔ A H = a . a . 2 a 2 + a 2 ) 2 = 6 a 3
Vậy d A C , S D = 6 a 3
Cách 2:

Dễ thấy D C ⊥ ( S A C ) . Trên mặt phẳng (ABCD)
dựng: A G / / C D , D G / / A C , D G ∩ A B = E
Dễ dàng chứng minh được: S.AED là tam diện vuông (1)
Tính được: AE=AD=2a.
Mà A C / / ( S D E )
⇒ d A C , S D = d A C , S D E = d A , S D E = A H
Với AH là đoạn thẳng dựng từ A vuông góc với mặt phẳng (ADE)
Ta có: 1 A H 2 = 1 S A 2 + 1 A E 2 + 1 A D 2
⇒ A H = 6 a 3
Cách 3:
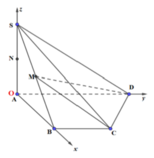
Gắn hệ trục tọa độ Oxyz

Khi đó A ( 0 ; 0 ; 0 ) ; C ( a ; a ; 0 ) ;
D ( 0 ; 2 a ; 0 ) ; S ( 0 ; 0 ; a )
Do đó A C ⇀ = ( a ; a ; 0 ) ; S D ⇀ = ( 0 ; 2 a ; - a ) ; S A ⇀ = ( 0 ; 0 ; - a ) ;
và A C ⇀ ; S D ⇀ = ( - a ; a ; 2 a )
Ta có d A C , S D = A C ⇀ ; S D ⇀ . S A ⇀ A C ; ⇀ S D ⇀
= - a . 0 + a . 0 + 2 a . ( - a ) - a 2 + a 2 + 2 a 2 = 6 a 3
Chọn đáp án C.
Đáp án C
Hướng dẫn giải: Do AD // BC
Kẻ AH ⊥ SB
Ta có B C ⊥ A B B C ⊥ S A
Mà A H ⊥ S B ⇒ A H ⊥ ( S B C )
⇒ A H ⊥ d ( A , ( S B C ) ) ta có: