Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:

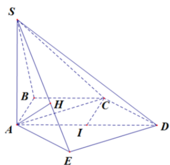
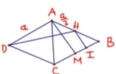
Gọi I là trung điểm của cạnh AD.
∆ A B C vuông cân tại B, ∆ I C D vuông cân tại I và có AB=IC=a nên A C = C D = a 2
Khi đó A C 2 + C D 2 = A D 2 nên ∆ A C D vuông cân tại C.
Trong (ABCD), dựng hình vuông ACDE. Trong ∆ S A E , kẻ A H ⊥ S E ( 1 )
Ta có
E D ⊥ S A E D ⊥ A E ⇒ E D ⊥ ( S A E ) ⇒ E D ⊥ A H ( 2 )
Từ (1) và (2) suy ra A H ⊥ ( S D E )
Vì A C / / E D nên
d A C , S D = d A C , S D E = d A ; S D E = A H
Trong ∆ S A E , 1 A H 2 = 1 S A 2 + 1 A E 2
⇔ A H = S A . A E S A 2 = A E 2 ⇔ A H = a . a . 2 a 2 + a 2 ) 2 = 6 a 3
Vậy d A C , S D = 6 a 3
Cách 2:

Dễ thấy D C ⊥ ( S A C ) . Trên mặt phẳng (ABCD)
dựng: A G / / C D , D G / / A C , D G ∩ A B = E
Dễ dàng chứng minh được: S.AED là tam diện vuông (1)
Tính được: AE=AD=2a.
Mà A C / / ( S D E )
⇒ d A C , S D = d A C , S D E = d A , S D E = A H
Với AH là đoạn thẳng dựng từ A vuông góc với mặt phẳng (ADE)
Ta có: 1 A H 2 = 1 S A 2 + 1 A E 2 + 1 A D 2
⇒ A H = 6 a 3
Cách 3:
Gắn hệ trục tọa độ Oxyz

Khi đó A ( 0 ; 0 ; 0 ) ; C ( a ; a ; 0 ) ;
D ( 0 ; 2 a ; 0 ) ; S ( 0 ; 0 ; a )
Do đó A C ⇀ = ( a ; a ; 0 ) ; S D ⇀ = ( 0 ; 2 a ; - a ) ; S A ⇀ = ( 0 ; 0 ; - a ) ;
và A C ⇀ ; S D ⇀ = ( - a ; a ; 2 a )
Ta có d A C , S D = A C ⇀ ; S D ⇀ . S A ⇀ A C ; ⇀ S D ⇀
= - a . 0 + a . 0 + 2 a . ( - a ) - a 2 + a 2 + 2 a 2 = 6 a 3
Chọn đáp án C.


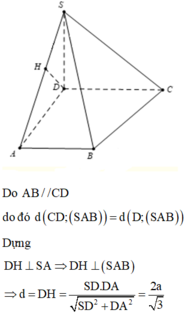
Ta có S C D ∩ A B C D = C D
C D ⊥ S A C D ⊥ A C ⇒ C D ⊥ S A C ⇒ S C ⊥ C D
Vì S C ⊥ C D , S C ⊂ S C D A C ⊥ C D , A C ⊂ A B C D
Nên S C D , A B C D ^ = S C A ^ = 45 o
Dễ thấy ∆ S A C vuông cân tại A
Suy ra SA = AC = a 2
Lại có
S M C D = 1 2 M C . M D = 1 2 a . a = a 2 2
Do đó
V = V S . M C D = 1 3 S M C D S A = 1 3 . a 2 2 . a 2 = a 3 2 6
Ta có
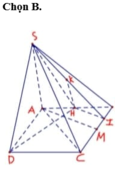
B D ∥ M N M N ⊂ S M N ⇒ B D ∥ S M N
Khi đó d( SM,BD ) = d( SM, (SMN) ) = d( D, (SMN) ) = d( A, ( SMN) )
Kẻ A P ⊥ M N , P ∈ M N A H ⊥ S P , H ∈ S P
Suy ra A H ⊥ S M N ⇒ d A S M N = A H
∆ S A P vuông tại A có
1 A H 2 = 1 S A 2 + 1 A P 2 = 1 S A 2 + 1 A N 2 + 1 A M 2 = 1 2 a 2 + 1 a 2 4 + 1 a 2 = 11 2 a 2
Do đó d = d( SM, BD ) = AH = a 22 11
Đáp án A

Đáp án D.
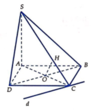
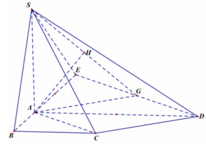
Trong mp A B C D gọi O là giao điểm của AC và BD.
Trong mặt phẳng S A C , qua O kẻ đường thẳng vuông góc với SC, cắt SC tại H.
Ta có B D ⊥ A C B D ⊥ S A ⇒ B D ⊥ S A C ⇒ B D ⊥ O H ⇒ O H là đường vuông góc chung của hai đường thẳng SC và BD.
Lại có A C = a 2 ⇒ C S = S A 2 + A C 2 = a 2 + 2 a 2 = 3 a 2 = a 3 .
Hai tam giác COH và CSA đồng dạng với nhau. Suy ra
O H S A = C O C S ⇒ O H = S A . C O C S = a . a 2 2 a 3 = a 6 6
Vậy khoảng cách giữa hai đường thẳng SC và BD bằng a 6 6 .
Chọn đáp án D.

Đáp án D
Phương pháp: Đưa khoảng cách từ M đến (SAC) về khoảng cách từ H đến (SAC).
Cách giải: Gọi H là trung điểm của AB ta có SH ⊥ (ABCD)
Ta có (SC;(ABCD)) = (SC;HC) = Góc SCH = 45 0
=>∆SHC vuông cân tại H => 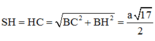
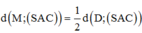
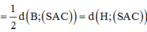
Trong (ABD) kẻ HI ⊥ AC,trong (SHI) kẻ HK ⊥ SI ta có:
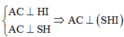
![]()
![]()
Ta có ∆AHI: ∆A CB(g.g) => 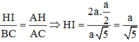
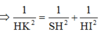
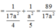
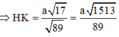





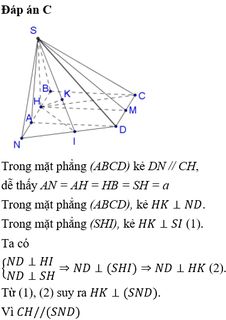


HD: Gọi I là trung điểm của AD → ABCI là hình vuông cạnh a → ∆ACI có đường trung tuyến