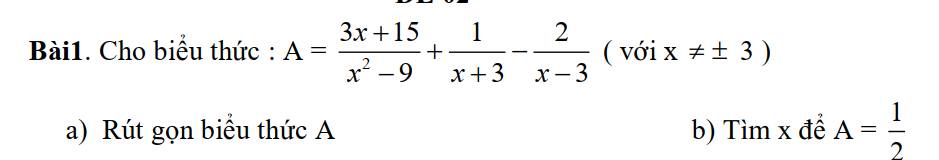Mong mn giúp đỡ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
Đỗ Thanh Hải
CTVVIP
14 tháng 6 2021
41 in
42 from
43 have
44 are
45 my
46 His
47 whenever
48 to
49 am
50 me
Mong mn giúp đỡ
21 tháng 5 2021
\(f\left(x\right)=x^2-\left(2m-1\right)x-2\sqrt{x}+m^2-2m\)
1) đk: \(x\ge0\)
Thay m=2 vào \(f\left(x\right)=0\) ta được: \(x^2-3x-2\sqrt{x}=0\)
\(\Leftrightarrow\)\(\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\\\sqrt{x}+1=0\left(vn\right)\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)(tm)
2) Thay m=6 vào f(x) ta được:
\(f\left(x\right)=x^2-11x-2\sqrt{x}+24\)
\(f\left(x\right)\le0\) \(\Leftrightarrow x^2-11x-2\sqrt{x}+24\le0\) (bước này coi \(\sqrt{x}\) là nghiệm thì sẽ trở thành bpt
bậc 4 ,bấm máy tính sẽ tìm được nghiệm)
\(\Leftrightarrow\)\(\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}-\dfrac{-1+\sqrt{17}}{2}\right)\left(\sqrt{x}+\dfrac{1+\sqrt{17}}{2}\right)\le0\)
mà \(\sqrt{x}\ge0\) \(\Rightarrow\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}+\dfrac{1+\sqrt{17}}{2}>0\end{matrix}\right.\)
bpt \(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}-\dfrac{-1+\sqrt{17}}{2}\right)\le0\)
\(\Leftrightarrow\sqrt{x}\in\left[\dfrac{-1+\sqrt{17}}{2};3\right]\)
\(\Leftrightarrow x\in\left[\dfrac{9-\sqrt{17}}{2};9\right]\)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Lời giải:
a.
$A=\frac{3x+15}{(x-3)(x+3)}+\frac{x-3}{(x+3)(x-3)}-\frac{2(x+3)}{(x-3)(x+3)}$
$=\frac{3x+15+(x-3)-2(x+3)}{(x+3)(x-3)}=\frac{2x+6}{(x-3)(x+3)}$
$=\frac{2(x+3)}{(x-3)(x+3)}=\frac{2}{x-3}$
b.
Để $A=\frac{1}{2}$
$\Leftrightarrow \frac{2}{x-3}=\frac{1}{2}$
$\Leftrightarrow x-3=4$
$\Leftrightarrow x=7$ (tm)
MN
11
