Xác định giá trị thực k để hàm số f x = x 2016 + x - 2 2018 x + 1 - x + 2018 , x ≠ 1 k , x = 1 liên tục tại x = 1.
A. k = 1
B. k = 2 2019
C. k = 2017 . 2018 2
D. 20016 2017 2019
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Cách1: Tư duy tự luận
Hàm số liên tục tại điểm x = 1 khi lim x → 1 f x = f 1 .
Ta có f 1 = k và lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 .
= lim x → 1 x 2016 − x + 2 x − 1 2018 x + 1 + x + 2018 2018 x + 1 − x + 2018 2018 x + 1 + x + 2018
= lim x → 1 x x − 1 x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 x − 1
= lim x → 1 x x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 = 2015 + 2 .2 1019 2017
= 2 2019
Vậy để hàm số liên tục tại điểm x=1 khi k = 2 2019
Cách 2: Tư duy tự luận (tính giới hạn bằng công thức L’Hospital)
Ta có
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = lim x → 1 2016 x 2015 + 1 1009 2018 x + 1 − 1 2 x + 2018
= 2016 + 1 1009 2019 − 1 2 2019 = 2 2019
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .
Cách 3: Sử dụng máy tính cầm tay (casio và vinacal)
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = 2 2019 .
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .

Chọn D
Phương pháp:
Biến đổi phương trình về f(x) = 2018 - m và sử dụng tương giao đồ thị: Phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng y = 2018 - m cắt đồ thị hàm số y = f(x) tại duy nhất một điểm.
Cách giải:
Phương trình f(x) + m - 2018 = 0 ![]()
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 - m (có phương song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt 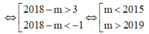

Chọn C
Đồ thị hàm số y= f’( x+ 2018) là phép tịnh tiến của đồ thị hàm số y= f’(x) song song với trục hoành về bên trái 2018 đơn vị.
=> đồ thị hàm số y= f’( x+ 1018) vẫn cắt trục hoành tại 3 điểm.
Đáp án B
Để f(x) liên tục tại x = 1 thì lim x → 1 f ( x ) = f ( 1 ) . Ta có:
lim x → 1 f ( x ) = l i m x 2016 + x - 1 2018 x + 1 - x + 2018 = lim x → 1 2016 x + 1 1009 2018 x + 1 - 1 2 x + 2018 = 2 2019
Vậy k = 2 2019 .