Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
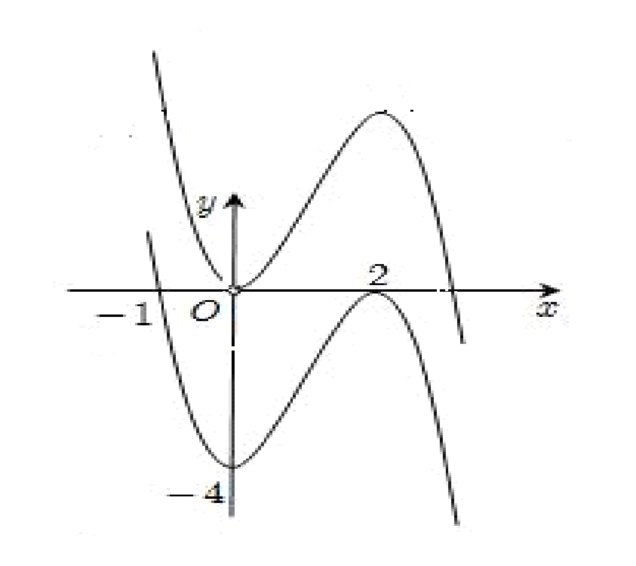
Ta có: ![]() có đồ thị là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương Oy lên trên 4 đơn vị.
có đồ thị là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương Oy lên trên 4 đơn vị.
Khi đó đồ thị hàm số y= f( x) + 4x cắt trục hoành tại 1 điểm.
ta chọn đáp án A.

Chọn A
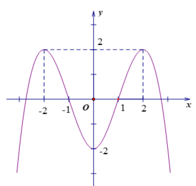
Cách 1: Từ đồ thị hàm số của ![]() ta thấy
ta thấy ![]() có hai cực trị dương nên hàm số
có hai cực trị dương nên hàm số ![]() lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm giao điểm của đồ thị hàm số
lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm giao điểm của đồ thị hàm số ![]() với trục tung nữa ta được tổng cộng là
với trục tung nữa ta được tổng cộng là ![]() cực trị.
cực trị.

Chọn B
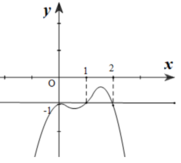
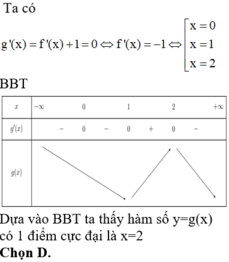
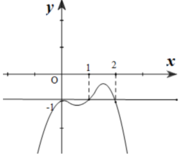
Ta có g’(x) = f’(x) + 1.
Đồ thị của hàm số y= g’(x) là phép tịnh tiến đồ thị của hàm số y= f’(x) theo phương song song với Oy lên trên 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x) cắt trục hoành tại hai điểm phân biệt.
=> Hàm số y= g(x) có 2 điểm cực trị.

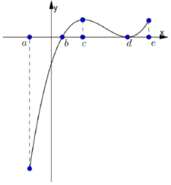
Ta có bảng biến thiên như hình vẽ sau:
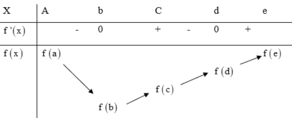
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.

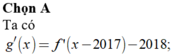
![]()
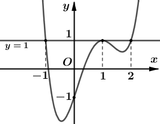
Dựa vào đồ thị hàm số y= f’(x) suy ra phương trình f’( x- 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số y= g( x) có 1 điểm cực trị

Chọn C.
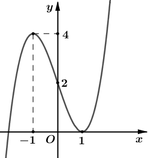
Vì đề bài hỏi điểm cực tiểu của đồ thị hàm số, dựa hình vẽ ta thấy điểm ![]() là điểm cực tiểu của đồ thị hàm số.
là điểm cực tiểu của đồ thị hàm số.

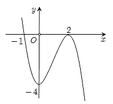

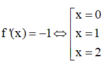
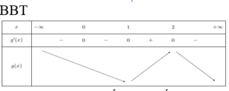
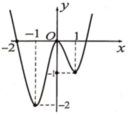
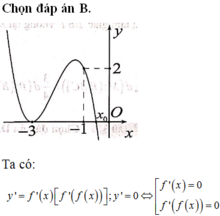
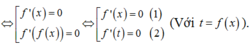
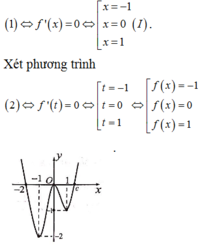
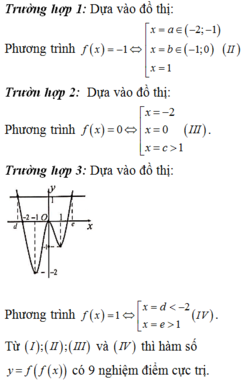
Chọn C
Đồ thị hàm số y= f’( x+ 2018) là phép tịnh tiến của đồ thị hàm số y= f’(x) song song với trục hoành về bên trái 2018 đơn vị.
=> đồ thị hàm số y= f’( x+ 1018) vẫn cắt trục hoành tại 3 điểm.