Vật thật AB vuông góc với trục chính của một thấu kính phân kì, tiêu cự f = -20cm. Ảnh A'B' qua thấu kính có A'B'=0,4AB. Xác định khoảng cách giữa vật và ảnh.
A. 36 cm.
B. 20 cm.
C. 18 cm.
D. 12 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

– Với d 1 = 12cm: ảnh ảo là : d 1 ’ = -30cm
- Với d 2 = -30cm: vật ảo là d 2 ’ = 12cm (không xét).

a. Dựng ảnh A'B'

b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm

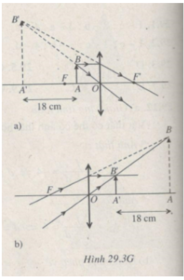
Trong mọi trường hợp (Hình 29.3G):
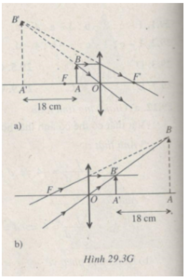
AA’ = |d + d’|
Do đó theo đề bài: |d + d’| = 18cm
Với d' = df/(d-f) = 20d/(d-f)
Ta suy ra
d + 20d/(d-f) = ±18
=> d 2 ±18 = ±360
Giải:
* d 2 – 18d + 360 = 0: phương trình vô nghiệm.
* d 2 + 18d – 360 = 0: có hai nghiệm.
Hai vị trí của vật:
d 1 = 12cm; d 2 = -30cm.
Chú ý: Phương trình d 2 – 18d + 360 = 0 ứng với vật thật - ảnh thật.
Ta biết khi đó A A ' m i n = 4f = 80cm
Do đó trị số AA’ = 18cm không phù hợp.

a) Do hứng được ảnh trên màn nên thấu kính đã sử dụng là thấu kính hội tụ.
b)
Đổi : \(AB=h=5\left(mm\right)=0,5\left(cm\right)\)
Xét \(\Delta OAB\sim\Delta OA'B'\) : \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\) (*)
Xét \(\Delta F'OI\sim\Delta F'A'B'\) : \(\dfrac{OI}{A'B'}=\dfrac{OF'}{F'A'}\).
Mà \(OI=AB\) và \(F'A'=OA'-OF'\) nên \(\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'-OF'}\).
Từ đó, suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\Leftrightarrow\dfrac{18}{d'}=\dfrac{12}{d'-12}\Leftrightarrow d'=36\left(cm\right)\)
Thay lại vào (*) ta được : \(\dfrac{18}{36}=\dfrac{0,5}{h'}\Leftrightarrow h'=1\left(cm\right)\)
Vậy : Ảnh ở vị trí cách thấu kính 36cm và cao 1cm.

Ta có: \(\Delta ABO\sim\Delta A'B'O\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\left(1\right)\)
Và \(\Delta OIF\sim\Delta A'B'F\Rightarrow\dfrac{OF}{A'F}=\dfrac{OI}{A'B'}\left(2\right)\)
\(\Rightarrow\dfrac{OF}{OF-OA'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{12}{12-OA'}=\dfrac{6}{OA'}\Rightarrow OA'=4\left(cm\right)\)
Ta có: \(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow A'B'=\dfrac{AB.OA}{OA'}=\dfrac{36.6}{4}=54\left(cm\right)\)
Vật ảnh cao 4cm và cách thấu kính 54cm
Chọn đáp án C.
Thấu kính phân kì ⇒ d ' < 0
Ta có A ' B = 0 , 4 A B ⇔ d ' = − 0 , 4 d
1 f = 1 d + 1 d ' ⇔ 1 − 20 = 1 d − 1 0 , 4 d ⇔ d = 30 c m ⇒ d ' = − 12 c m . Khoảng cách giữa vật và ảnh là L = d + d ' = 18 c m .