Trong khai triển Newton của biểu thức
2
x
-
1
2019
, số hạng chứa
x
18
là ...
Đọc tiếp
Trong khai triển Newton của biểu thức 2 x - 1 2019 , số hạng chứa x 18 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
4 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
CM
15 tháng 10 2018
Chọn D
Số hạng tổng quát trong khai triển ( 2 x - 1 ) 2019 là
Theo đề bài ta có: 2019 - k = 18 => k = 2001.
Vậy trong khai triển biểu thức đã cho, số hạng chứa x 18 là:
CM
18 tháng 10 2018
Chọn B
Ta có:
(
2
x
-
1
)
2019
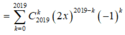
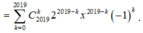
Số hạng tổng quát của khai triển là 
.
Để có x 18 thì 2019 - k = 18 => k = 2001.
Khi đó số hạng chứa
x
18
là 
.
PT
Số hạng không chứa x trong khai triển Newton của biểu thức x 2 − 2 x 3 7 là
A. -84
B.-448
C.84
D.448
1
CM
19 tháng 2 2018
Đáp án D
Số hạng tổng quát trong khai triển
T k+ 1 = C 7 k x 2 k − 2 x 3 7-k = C 7 k x 2 k − 2 x 1 3 7-k = C 7 k x 2 k ( − 2 ) 7-k x 7 − k 3 = C 7 k x 2 k ( − 2 ) 7-k x 7 − k 3 = C 7 k x 7 k − 7 3 ( − 2 ) 7-k
số hạng không chứa x ứng với k: 7 k − 7 3 = 0 ⇔ k=1
Vậy số hạng không chứa x là: C 7 1 ( − 2 ) 7-1 = 448
Vậy P A = 1 5040
PT
1
CM
10 tháng 6 2019
Đáp án D
Số hạng tổng quát trong khai triển
T k+ 1 = C 7 k x 2 k − 2 x 3 7-k = C 7 k x 2 k − 2 x 1 3 7-k = C 7 k x 2 k ( − 2 ) 7-k x 7 − k 3 = C 7 k x 2 k ( − 2 ) 7-k x 7 − k 3 = C 7 k x 7 k − 7 3 ( − 2 ) 7-k
số hạng không chứa x ứng với k: 7 k − 7 3 = 0 ⇔ k=1
Vậy số hạng không chứa x là: C 7 1 ( − 2 ) 7-1 = 448
Vậy P A = 1 5040
JL
1
7 tháng 4 2023
SHTQ là: \(C^k_4\cdot\left(x^3\right)^{4-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_4\cdot x^{12-4k}\)
Số hạng ko chứa x tương ứng với 12-4k=0
=>k=3
=>SH đó là \(C^3_4=4\)
