Tìm x, biết rằng 3.(10x) =111
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
26 tháng 10 2017
a)
3 . ( 10 . x ) = 111
3 . 10 . x = 111
30 . x = 111
x = \(\frac{37}{10}\)
b) 3 + ( 10 . x ) = 111
10 . x = 111 - 3
10 . x = 108
x = 108 : 10
x = 10.8
26 tháng 10 2017
3. ( 10.x ) = 111
10.x = 111 : 3
10.x = 37
x = 37 : 10
x = 3,7
______________________
3 + ( 10.x ) = 111
10.x = 111 - 3
10.x = 108
x = 108 : 10
x = 10,8
CM
16 tháng 8 2018
3 + (10.x) = 111
10.x = 111- 3
10.x = 108
x = 108:10
x = 10,8
CM
10 tháng 11 2018
3 + (10 + x ) = 111
10 + x = 111- 3
10 + x = 108
x = 108 – 10
x = 98
CM
22 tháng 4 2017
3.(10 + x) = 111
10+ x = 111: 3
10 + x = 37
x = 37 – 10
x = 27
A
24 tháng 6 2019
a, \(3.\left(10.x\right)=111\Leftrightarrow\left(10.x\right)=111:3\)
\(\Leftrightarrow10.x=37\Leftrightarrow x=37:10\Leftrightarrow x=3,7\)
b,\(3.\left(10+x\right)=111\Leftrightarrow\left(10+x\right)=111:3\)
\(\Leftrightarrow10+x=37\Leftrightarrow x=37-10\Leftrightarrow x=27\)
c,\(3+\left(10.x\right)=111\Leftrightarrow\left(10.x\right)=111-3\)
\(\Leftrightarrow10.x=108\Leftrightarrow x=108:10\Leftrightarrow x=10,8\)
d,\(3+\left(10+x\right)=111\Leftrightarrow\left(10+x\right)=111-3\)
\(\Leftrightarrow10+x=108\Leftrightarrow x=108-10\Leftrightarrow x=98\)
9 tháng 6 2017
a) \(3.\left(10.x\right)=111\)
\(10.x=37\)
\(x=\dfrac{37}{10}\)
b) \(3.\left(10+x\right)=111\)
\(10+x=37\)
\(x=27\)
c) \(3+\left(10.x\right)=111\)
\(10.x=108\)
\(x=\dfrac{54}{5}\)
d) \(3+\left(10+x\right)=111\)
\(x=111-3-10\)
\(x=98\)
AH
Akai Haruma
Giáo viên
5 tháng 9 2020
Lời giải:
Ta thấy:
$10x\equiv 0\pmod 5$
$288\equiv 3\pmod 5$
$\Rightarrow y^2\equiv 3\pmod 5$ (vô lý)
Do ta biết rằng một số chính phương khi chia cho $5$ chỉ có thể có dư là $0,1,4$.
Như vậy, không tồn tại số tự nhiên $x,y$ thỏa mãn điều kiện đề bài.
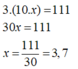
3.(10x) = 111
10.x = 111 : 3
10.x = 37
x = 37 : 10
x = 3,7