K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
26 tháng 10 2017
a)
3 . ( 10 . x ) = 111
3 . 10 . x = 111
30 . x = 111
x = \(\frac{37}{10}\)
b) 3 + ( 10 . x ) = 111
10 . x = 111 - 3
10 . x = 108
x = 108 : 10
x = 10.8
26 tháng 10 2017
3. ( 10.x ) = 111
10.x = 111 : 3
10.x = 37
x = 37 : 10
x = 3,7
______________________
3 + ( 10.x ) = 111
10.x = 111 - 3
10.x = 108
x = 108 : 10
x = 10,8
CM
16 tháng 8 2018
3 + (10.x) = 111
10.x = 111- 3
10.x = 108
x = 108:10
x = 10,8
CM
10 tháng 11 2018
3 + (10 + x ) = 111
10 + x = 111- 3
10 + x = 108
x = 108 – 10
x = 98
CM
22 tháng 4 2017
3.(10 + x) = 111
10+ x = 111: 3
10 + x = 37
x = 37 – 10
x = 27
9 tháng 6 2017
a) \(3.\left(10.x\right)=111\)
\(10.x=37\)
\(x=\dfrac{37}{10}\)
b) \(3.\left(10+x\right)=111\)
\(10+x=37\)
\(x=27\)
c) \(3+\left(10.x\right)=111\)
\(10.x=108\)
\(x=\dfrac{54}{5}\)
d) \(3+\left(10+x\right)=111\)
\(x=111-3-10\)
\(x=98\)
11 tháng 12 2016
10x=6y=>x/6=y/10=>2x^2/72=y^2/100
áp dụng tính chất dãy tỉ số bang nhau ta có
\(^{2x^2}_{72}\)=\(^{y^2}_{100}\)=2x^2-y^2/72-100=-28/-28=1
=>x=6,y=10
24 tháng 2 2018
Vì |10x-3|1975\(\ge\)0
|2y-9|1945\(\ge\)0
=> (10x-3)1975+(2y-9)1945=0
<=> \(\hept{\begin{cases}10x-3=0\\2y-9=0\end{cases}}\)
<=>\(\hept{\begin{cases}x=\frac{3}{10}\\y=\frac{9}{2}\end{cases}}\)
H
4 tháng 4 2023
\(a,3x^2-3x\left(x-2\right)=36\\ \Leftrightarrow3x^2-3x^2+6x=36\\ \Leftrightarrow6x=36\\ \Leftrightarrow x=6\\ b,5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x+2\right)=-36\\ \Leftrightarrow20x^3-10x^2+5x-20x^3+10x^2-4x+36=0\\ \Leftrightarrow\left(20x^3-20x^3\right)+\left(-10x^2+10x^2\right)+\left(5x-4x\right)=-36\\ \Leftrightarrow x=-36\)
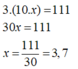
3.(10x) = 111
10.x = 111 : 3
10.x = 37
x = 37 : 10
x = 3,7