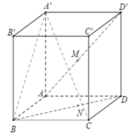
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD¢, điểm N thuộc đoạn BD sao cho AM=DN=x với 0 < x < a 2 2 . Tìm x theo a để đoạn MN ngắn nhất
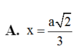
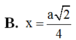
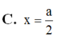
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

Kẻ:
M H ⊥ A D ⇒ M H = A H = x 2 2 ⇒ H D = a − x 2 2
Tam giác HND có
H N 2 = D N 2 − 2 D N . H D . c o s 2 N D H ^
= a − x 2 2 2 + x 2 − 2 x a − x 2 2 = 5 2 x 2 − 2 2 a x + a 2
Vì:
M H ⊥ A D ⇒ M H / / A A ' ⇒ M H ⊥ A B C D ⇒ M H ⊥ H N
Tam giác MHN vuông tại H, có M N 2 = M H 2 + H N 2
= x 2 2 2 + 5 2 x 2 − 2 2 a x + a 2 = 3 x 2 − 2 2 a x + a 2 = 1 3 x − a 2 3 2 + a 2 3 ≥ a 2 3 ⇒ M N ≥ a 3 3 ⇒ M N min = a 3 3
Dấu “=” xảy ra khi
x
=
a
2
3

Đáp án D
Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó
2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!

Lời giải: Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là 30 0 . Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc 30 0 , khi đó MN là đường trung bình của tam giác BA’P nên MN = 1 2 A'P.
Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ = a – x (tam giác PC’H vuông cân tại C’), và A'H = ![]()
Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) = 30 0 , do đó
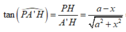
![]()
Mặt khác ta lại có A'P = ![]()
![]() (2)
(2)
Từ (1) và (2) ta tính được ![]()
Từ đây ta rút ra được![]()
=> Chọn phương án D.

Chọn B
* Sử dụng định lí Ta-lét đảo.
Ta có: ![]()
![]()
Áp dụng định lí Ta-lét đảo, ta có AD, MN, BD' lần lượt nằm trên ba mặt phẳng song song.
=> M song song với mặt phẳng (P) chứa BD' và song song với AD.
Nên MN//(BCD'A') hay MN//(A'BC)
* Sử dụng định lí Ta-lét.
* Sử dụng định lí Ta-lét.
Vì AD//A'D' nên tồn tại (P) là mặt phẳng qua AD và song song với mp (A'D'CB)
(Q) là mặt phẳng qua M và song song với mp (A'D'CB). Giả sử (Q) cắt DB tại N
Theo định lí Ta-lét ta có: ![]()
Mà các mặt của hình hộp là hình vuông cạnh a nên AD' = DB = a 2
Từ (*), ta có: AM = DN' => DN' = DN
![]()
(Q)//(A'D'CB) suy ra luôn song song với mặt phẳng cố định (A'D'CB) hay (A'BC)
Đáp án A